حل آخر

سنستخدم الصيغ:

Within groups ( SW2 )

Between groups  ( SB2 )

 Variance ( S2 )

 

نكون الجدول الآتي:

 

Class 1 Class 2 Class 3
X1 X1 – `X1 (X1 – `X1)2 X2 X2 – `X2 (X2 – `X2)2 X3 X3 – `X3 (X3 – `X3)2
66 – 8.2 67.24 96 19.6  384.16 58 – 15.4  237.16
65 – 9.2 84.64 87 10.6  112.36 62 – 11.4  129.96
88 13.8 190.44 66 – 10.4  108.16 77 3.6  12.96
92 17.8 316.84 55 – 21.4  457.96 90 16.6  275.56
60 – 14.2 201.64 78 1.6  2.56 80 6.6 43.56
371   860.8 382   1065.2 367   699.2

`X1= 74.2

 S12 = 860.8/4 = 215.2

  `X2= 76.4

 S22 = 1065.2/4 = 266.3

`X3= 73.4

  S32 = 699.2/4 = 174.8

 

باستخدام الصيغ السابقة نجد أن:

 SW2  = ( S12 + S22 + S32 ) / K

         = ( 215.2 + 266.3 + 174.8) / 3

         = 218.77

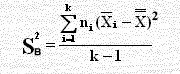
̿X = (74.2 + 76.4 + 73.4) / 3 = 74.667

 SB2  =5 [( 74.2 – 74.227 )2 + (  76.4 – 74.667 )2 + ( 73.4 – 74.667 )2 ] / ( 3 – 1 )

         = 5( 0.218 + 3.003 + 1.605) / 2

         = 24.13 / 2

         = 12.065

F = SB2 /  SW2

   = 12.065 / 218.77

   = 0.055 < 3.89

   إن قيمة F المحسوبة أقل من قيمة F الجدولية ولذا نقبل الفرضية الصفرية عند α = 0.05 بعدم وجود اختلاف بين المتوسطات.