المقارنات المتعددة Multiple Comparisons
هي طريقة لإجراء عدد من الاختبارات الأولية لتحديد الفروق المعنوية للمتوسطات حال رفض فرضية العدم.
حال رفض فرضية العدم عند مستوى معنوية فلا دليل على وجود فروق معنوية بين المتوسطات ولا نعرف أي منها يختلف عن متوسطات (العينات) ومن حيث قيمة F معنوية ففرق المشاهدات بين المتوسطات معنوي أيضاً وعلى العموم توجد عدة طرق إحصائية لعمل اختبار بهذا الخصوص مثل:
Scheffe Test, Student-Newman Keuls, Tukey's Procdure, Least Significant difference, Duncans New Multiple range
سنتعرض كل منها بصورة مبسطة مع مثال.
الطريقة Least Significant difference للمقارنة بين متوسطين
يرمز لها LSD وتحدد حال استخدام برنامج SPSS وتعرف Fisher's LSD وتختبر كل الأزواج فإن تمَ رفض فرضية العدم (تساوي المتوسطات) مقابل الفرضية البديلة (عدم تساوي المتوسطات) فإذا كان الفرق أكبر من LSD فنرفض فرض العدم، والصيغة الرياضية لحساب LSD حيث MSE متوسط مجموع المربعات (التباين) داخل المجموعات) هي:
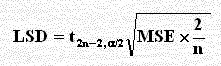
| A | B | C | D |
|
8 |
3 |
5 |
6 |
|
7 |
4 |
3 |
5 |
|
9 |
6 |
4 |
6 |
|
5 |
5 |
5 |
4 |
|
6 |
2 |
3 |
3 |
|
7 |
7 |
2 |
4 |
|
42 |
27 |
22 |
28 |
الحل: الحل باستخدام برنامج SPSS الحل باستخدام برنامج MINITAB الحل باستخدام برنامج EXCEL
نحسب مجموع المربعات الكلي ، مجموع المربعات داخل المجموعات لمصدر التباين كالتالي:
SST = ∑Xi2 – (∑X)2 / nk
= (8)2 + (7)2 + ... + (3)2 + (4)2 – (119)2 / 4× 6
= 669 – 590.042
= 78.958
SSW = ( ∑X2) / n – (X)2 / nk
= [(42)2 + (27)2 + (22)2 + (28)2] / 6 – (119)2 / 4× 6
= 626.833 – 590.042
= 36.791
جدول تحليل التباين
| Source of Variance | SS | d f | MS | F | f0.05,3,20 |
| SSB | SST – SSW = 36.791 | K – 1 = 4 – 1 = 3 | 12.264 | 5.818 | 3.10 |
| SSW | 42.167 | K(n – 1) = 4(6 – 1) = 20 | 2.108 | ||
| TOTAL | 78.958 | Kn – 1 = 24 – 1 = 23 |
قيمة F المحسوبة أكبر من F الجدولية ( 7.64 > 3.1 ) فالمتوسطات غير متساوية، وبإجراء اختبار LSD نجد أن
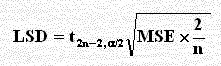
MSE × 2 / n = 3 × 2 ÷ 6 = 1 , t2n–2,α/2 = t10, 0.025 = 2.228
LSD = 2.228 × 1
= 2.228
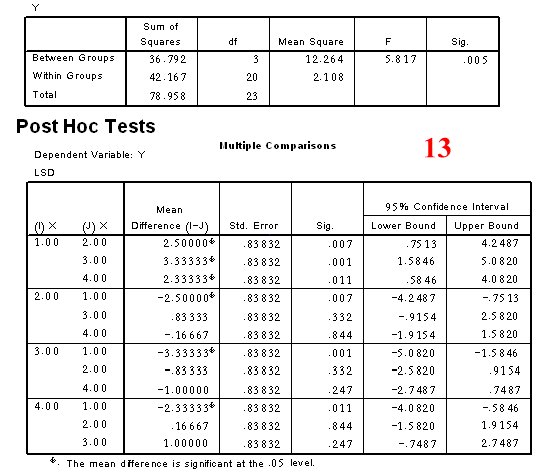
جدول متوسطات الفروق حيث وجود *على العدد يعني وجود فرق معنوي بين المتوسطين ولدينا أربع متوسطات (7، 4.5، 3.7، 4.7) تقارن كل منها بقيمة LSD = 2.228
| `X1 = 7 | `X2 = 4.5 | `X3 = 3.667 | `X4 = 4.667 | |
| `X1 = 7 | 0 | 2.5* | 3.333* | 2.333* |
| `X2 = 4.5 | ـــــ | 0 | 0.833 | – 0.167 |
| `X3 = 3.667 | ـــــ | ـــــ | 0 | – 1 |
| `X4 = 4.667 | ـــــ | ـــــ | ـــــ | 0 |
الشكل الآتي يبين طريقة الوصول للنتائج بإتباع تسلسل الأرقام والأسهم في الشكل:
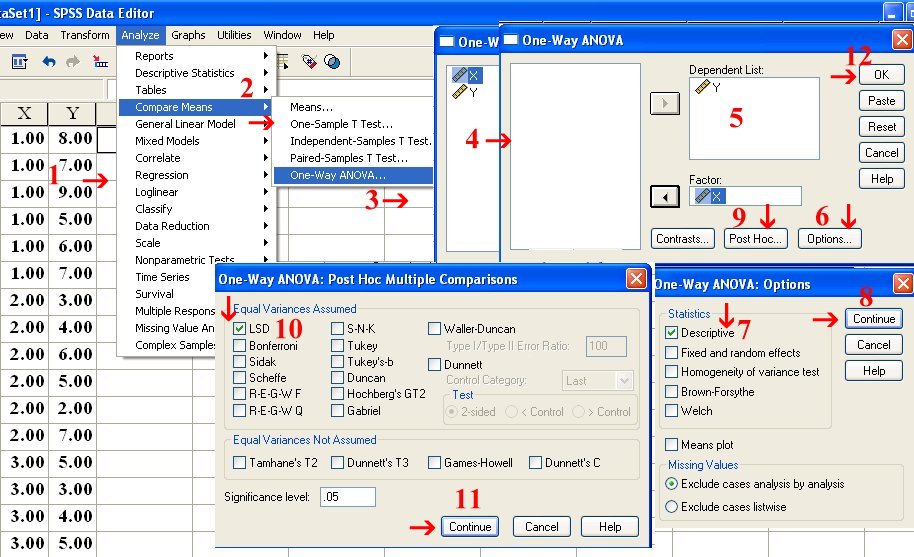
الشكل الآتي يبين طريقة الوصول للنتائج بإتباع تسلسل الأرقام والأسهم في الشكل:
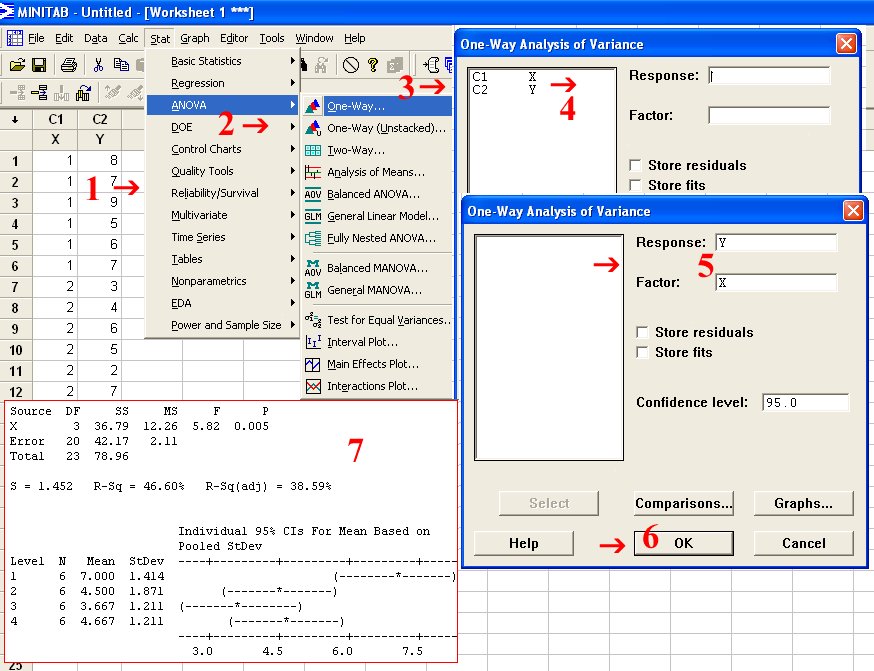
الشكل الآتي يبين طريقة الوصول للنتائج بإتباع تسلسل الأرقام والأسهم في الشكل: