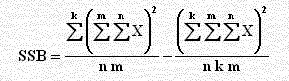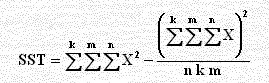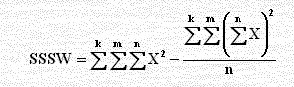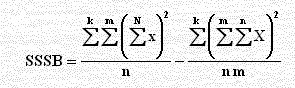تحليل التباين الأحادي مع أكثر من
مستوى واحد للمجموعة الواحدة
أولاً: تحليل التباين الأحادي مع مستويين لمجموعة واحدة
نستخدم الصيغ التالية:
|
مجموع مربعات التباين بين المجاميع SSB |
مجموع مربعات التباين الكلي SST |
|
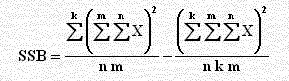 |
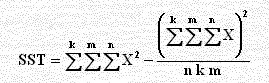 |
|
( SSW = WWT
– SSB ) حيث
SSW مجموع مربعات التباين ضمن المجاميع
|
|
مجموع مربعات التباين ضمن المجاميع الجزئية SSSW
|
مجموع مربعات التباين بين المجاميع الجزئية الواقعة
ضمن المجاميع SSSB
|
|
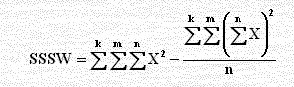 |
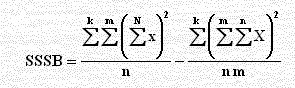 |
مما سبق نحصل على جدول تحليل التباين الأحادي لأكثر من مستوى
واحد وهو:
| Source Variance |
d f |
S S |
MS |
F |
| بين المجاميع |
k – 1 |
SSB |
SSB / (k –
1) |
MSSB / MSSSB |
| بين المجاميع الجزئية |
k ( m – 1 ) |
SSSB |
SSSB / k ( m
– 1 ) |
| ضمن المجاميع الجزئية |
k m ( n – 1
) |
SSSW |
SSSW / k ( N
– 1 ) |
MSSSB / MSSSW |
| المجموع الكلي |
k m n – 1 |
SST |
|
مثال:
فيما يلي تحصيل درجات مادة الرياضيات لفصلين
دراسيين، أخذنا درجات أربعة طلاب من ثلاثة صفوف من كل فصل دراسي. هل هناك فروق
معنوية لمتوسط تحصيل درجات الطلاب للفصلين (Term1,2) بين
صفوف الدراسة (Classes).
|
رموز |
المجاميع |
| Classes (k = 3) |
Class
1 |
Class
2 |
Class
3 |
| Students (m = 4) |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
|
Term 1 |
65 |
70 |
85 |
68 |
59 |
66 |
90 |
88 |
75 |
84 |
69 |
68 |
|
n=2 Term 2 |
65 |
80 |
92 |
75 |
62 |
60 |
85 |
90 |
70 |
79 |
72 |
70 |
|
n
المجاميع الجزئية X∑ |
125 |
150 |
167 |
143 |
121 |
126 |
175 |
178 |
145 |
163 |
141 |
138 |
|
m n
∑ ∑X |
585 |
600 |
578 |
الحل:
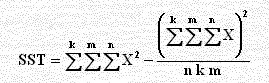
SST = [(60)2
+ (70)2 + (85)2 + ... + (72)2 + (70)2]
– [(
585 + 600 + 587)2] / (2×3×4)
= 133064 – (3139984
/ 24)
= 133064 – 130832.7
= 2231.333
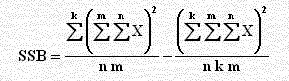
SSB = [[(585)2 +
(600)2 + (587)2]
/ (2×4)]
– [( 585 + 600 +
587)2] / (2×3×4)
= ( 342225 + 360000 + 344569) / 8 – (3139984
/ 24)
= 130849.3 – 130832.7
= 16.583
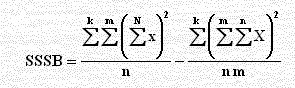
SSSB = [(125)2 + (150)2 +
(167)2 + ... + (141)2 + (138)2]
/ 2 – [[(585)2
+ (600)2 + (587)2]
/ (2×4)]
= 265808 / 2 – ( 342225 + 360000 + 344569) / 8
= 132904 – 130849.3
= 2054.7
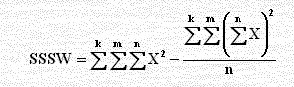
SSSW = [(60)2 + (70)2 + (85)2
+ ... + (72)2 + (70)2]
– [(125)2 + (150)2
+ (167)2 + ... + (141)2 + (138)2]
/ 2
= 133064 – 265808 / 2
= 133064 – 132904
= 160
جدول
تحليل التباين
| Source Variance |
d f |
S S |
MS |
F |
| بين المجاميع |
3
– 1 = 2 |
SSB = 16.583 |
16.583 / 2 = 8.292 |
16.583 / 2054.7 =
0.008 |
| بين المجاميع الجزئية |
3 ( 4 – 1 )
= 9 |
SSSB = 2054.7 |
2054.7 / 9
= 228.3 |
| ضمن المجاميع الجزئية |
3 × 4 × (2
– 1 ) = 12 |
SSSW = 160 |
160 / 12 =
13.333 |
2054.7 / 160 =
12.842 |
| المجموع الكلي |
3 × 4 × 2
– 1 = 23 |
SST = 2231.333 |
|
عند مستوى معنوية
α1
= 0.01 نجد أن:
Fα1/2,(2,9)
= 10.11 وعند مستوى
معنوية
α2
= 0.02 نجد أن: α2/2,(9,12)
= 4.935
وعليه يكون: i10.11
>
0.008
يعني عدم وجود فروق بين الصفوف
ولكن نجد أن: i12.842
>
4.935مما
يعني وجود فروق جوهرية بين الدرجات ضمن الصفوف خلال الفصلين الدراسيين.