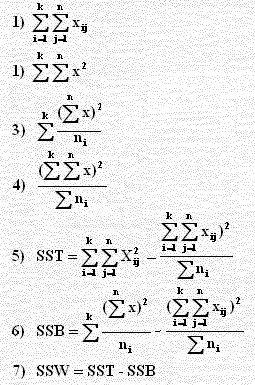
تحليل التباين الأحادي حال عدم تساوي حجم العينات
بنفس الطريقة السابقة (تساوي حجم العينات) حسب الصيغ الآتية:
مثال 1:
يمثل الجدول التالي نتائج طلبة تم تدريسهم مادة الإحصاء بأربعة طرق تدريس مختلفة أختبر الفرضية القائلة بتساوي متوسطات الطلبة وفق الاختبارات الأربعة عند مستوى معنوية 0.10
| M1 | M2 | M3 | M4 |
| 65 | 75 | 59 | 94 |
| 87 | 69 | 78 | 89 |
| 73 | 83 | 67 | 80 |
| 79 | 81 | 62 | 88 |
| 81 | 72 | 83 | 90 |
| 96 | 79 | 76 | |
| 90 |
الحل:
نضيف للجدول بعض القيم الأخرى لنحصل على
| M1 | M2 | M3 | M4 |
| 65 | 75 | 59 | 94 |
| 87 | 69 | 78 | 89 |
| 73 | 83 | 67 | 80 |
| 79 | 81 | 62 | 88 |
| 81 | 72 | 83 | 90 |
| 96 | 79 | 76 | |
| 90 | |||
| 481 | 549 | 425 | 441 |
الفرضية: Ho : μ1 = μ2 = μ , H1 : μ1 ≠ μ2 ≠ μ
نوجد كل مما يأتي حسب الترتيب: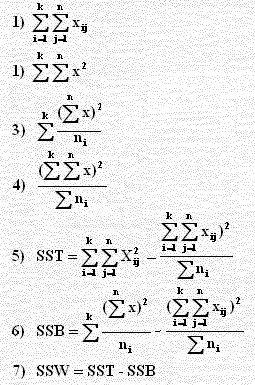
1) مجموع العناصر
2) مجموع مربعات العناصر
3) مجموع مربعات العناصر مقسوماً على حجم العينة
4)معامل التصحيح
5) مجموع مربعات التباين (SST)
6) مربعات التباين بين المجموعات ( SSB)
7) مربعات التباين ضمن المجموعات ( SSW)
وحسب الخطوات السبعة أعلاه نجد الآتي:

وتكون نتائج التحليل كالآتي:
|
مصدر التباين Source of Variance |
مجموع المربعات Sum of squares (SS) |
درجات الحرية df |
متوسط مجموع المربعات أو التباين Mean squares (MS) |
F (المحسوبة) Calculated |
F (الجدولية) Tabulated (Sig.) |
|
بين المجموعات Between Groups |
SSB = 833.819 |
K – 1 = 4 – 1 = 3 |
SB2 = 833.819/3 = 277.940 |
SB2 / SW2 277.940/72.409 = 3.839 |
Fα (K – 1) , (N – K) Fα(3,20) = 2.38
|
|
داخل المجموعات Within Groups (Error) |
SSW = 1448.181 |
N – K = 24 – 4 = 20 |
SW2 = 1448.181/20 = 72.409 |
||
|
المجموع Total |
SST = SSB + SSW = 2282 |
N – 1 = 24 – 1 = 23 |
|
وعند مستوى معنوية 0.10 نجد أن F الجدولية ( Fα(3,20) = 2.38 ) أقل من F المحتسبة فنرفض H0 مما يعني وجود فروق بين المتوسطات.