أسئلة وأجوبة (2)

الأمثلة:    (2)    (3)    (4)    (5)    (6)    (7)

(1) فيما يلي درجات 26 طالباً في الصف الأول الثانوي في مادة الرياضيات

    30    25    14    13    14    12    25    22    11    12    23    24    30

    18    17    16    12    25    14    19    20    20    30    29    28    27

    والمطلوب:

        1) كون الجدول التكراري المناسب متضمن التكرار النسبي، التكرار المئوي 

        2) ما هي نسبة الطلاب التي تزيد درجاتهم عن 20 درجة

الحـــل:   

الفئات العلامات التكرار التكرار النسبي التكرار المئوي
15 > /////    /// 8

8 ÷ 26 = 0.3077

(8 ÷ 26) × 100 = 30.77%
15 - 20 //// 4 0.1538

15.38%
20 - 25 ///// 5 0.1923

19.23%
25 - 30 /////   / 6 0.2308

23.08%
30 ≤ /// 3 0.1154

11.54%
المجموع   26 1

100.00%

 

أو بدون العلامات

 

RF %

Relative Frequency (RF)

Frequency (F)

Interval (X)

(8 ÷ 26) × 100 = 30.77%

8 ÷ 26 = 0.3077

 8 Less Than 15

15.38%

 0.1538 4 15 - 20

19.23%

 0.1923 5 20 - 25

23.08%

 0.2308 6 25 - 30

11.54%

 0.1154 3 More Than 30

100.00%

 1 26 Total

 

نسبة الطلاب التي تزيد درجاتهم عن عشرين درجة هي:

  53.85% = (14 ÷ 26) × 100

 

(2) إذا كان لدينا درجات مجموعتين من الطلاب في اختبار ما هي:

المجموعة الضابطة:  17    16    11    10    15    18    16    14    16    12
المجموعة التجريبية:  11    20    15    14    10     13    17    18    10    10    11    13  

            المطلوب إنشاء جدول تكراري مزدوج.

 الحـــل:   

التكرار العلامات الفئات
التجريبية الضابطة التجريبية الضابطة
6 5 /////    / ///// 10 - 15
7 5 /////    // ///// 16 - 21

أو

التكرار الفئات
التجريبية الضابطة
6 5 10 - 15
7 5 16 - 21

 

 

(3) الجدول التالي يبين استهلاك السجاير وقيمتها لمجموعة من الأفراد عددها 15والمطلوب إنشاء جدول تكراري مزدوج.

 

4 9 6 8 11 15 10 2 6 5 9 10 12 7 8 الاستهلاك
2 11 3 5 7 13 9 1 4 3 5 6 7 4 5 القيمة

الحـــل:

    نوجد أطوال الفئات وعددها

بالنسبة للاستهلاك: المدى = 15 – 2 + 1 = 14 ، عدد الفئات = 1 + 3.22لـو(15) = 4.91 ≈ 5، طول الفئة = 14 ÷ 5 = 2.8 ≈ 3

بالنسبة للقيمـــــــة: المدى = 13 – 1 + 1 = 13 ، عدد الفئات = 1 + 3.22لـو(15) = 4.91 ≈ 5، طول الفئة = 13 ÷ 5 = 2.6 ≈ 3

نكون الجدول المزدوج حيث الاستهلاك عموديا والقيمة أفقياً كالتالي:

الجدول التكراري المزدوج

المجموع

13 - 15

10 - 12

7 - 9

4 - 6

1 - 3

  →   فئات القيمة

↓  فئات الاستهلاك

2         // 2 - 4
4       // // 5 - 7
6   / / ////    8 - 10
2     //     11- 13
1 /         14- 16
15 1 1 3 6 4 المجموع

 

يمكن إعادة كتابة الجدول السابق بحذف العلامات كما يلي:

الجدول التكراري المزدوج

المجموع

13 - 15

10 - 12

7 - 9

4 - 6

1 - 3

  →   فئات القيمة

↓  فئات الاستهلاك

2         2 2 - 4
4       2 2 5 - 7
6   1 1 4    8 - 10
2     2     11- 13
1 1         14- 16
15 1 1 3 6 4 المجموع

 

 

(4) أكتب ما تعرفه عن الفئة 15 ــ 19؟ ، وكذلك عن الحدود الفعلية للفئة؟

       أولاً: إذا كانت الفئة لأعداد صحيحة كعدد السكان أو الوفيات

       ثانياً: إذا كانت الفئة لأعداد كالعمر والطول والوزن

    الحدود الفعلية للفئات

        لكل فئة حد أدنى (بدايتها) وحد أعلى (نهايتها) وقد يكونا أعداد صحيحة (ننقص 0.5) أو كسرية (ننقص 0.05 لرقم عشري واحد ، 0.005 لرقمين عشريين وهكذا)

        الأعداد الصحية كما سبق في الفئة السابقة 15 ــ 19 ، الحد الفعلي الأدنى = الحد الأدنى للفئة – 0.5 ، الحد الفعلي الأعلى = الحد الأعلى للفئة + 0.5

        الأعداد العشرية:

             للفئة 12.1 ــ 15.1 يكون الحد الفعلي الأدنى = 12.1 – 0.05 = 12.05 والحد الفعلي الأعلى = 15.1 + 0.05 = 15.15 (إضافة الرقم 5 أمام العدد)

            للفئة 12.45 ــ 15.45 يكون الحد الفعلي الأدنى = 12.45 – 0.005 = 12.445 والحد الفعلي الأعلى = 15.45 + 0.005 = 15.455

            للفئة 12.415 ــ 15.415 يكون الحد الفعلي الأدنى = 12.415 – 0.0005 = 12.4145 والحد الفعلي الأعلى = 15.415 + 0.0005 = 15.4155

لاحظ: الحد الفعلي الأعلى ينتج من إضافة الرقم 5 أمام العدد (يمينه) في حين الحد الفعلي الأدنى ينتج بطرح 1 من الجزء العشري ثم وضع 5 على يمين العدد كالتالي:

 

Exact Upper Limits Exact Lower Limits Upper Limits Lower Limits Interval
12.15 1 – 1 =0 , 10.05 12.1 10.1 10.1 – 12.1
20.45 4 – 1 = 3 , 16.35 20.4 16.4 16.4 – 20.4
35.245 24 – 1 = 23 , 32.235 35.24 32.24 32.24 – 35.24
0.225 18 – 1 = 17 , 0.175 0.22 0.18 0.18 – 0.22

 

للحد الفعلي الأدنى نأخذ الجزء العشري كعدد صحيح ونضربه × 10 ونطرح من الناتج 5 ونستبدله بالجزء العشري الأصلي

 فمثلاً 0.18 نأخذ 18 نضربها × 10 فنحصل على 180 نطرح 5 نحصل على 175 نجعلها بدل 18 في 0.18 فيكون الحد الفعلي الأدنى = 0.175

ومثلاً 16.4 نأخذ 4 نضربها × 10 فنحصل على 40 نطرح 5 نحصل على 35 نجعلها بدل 4 في 16.4 فيكون الحد الفعلي الأدنى = 16.35

ومثلاً 32.24  نأخذ 24 نضربها × 10 فنحصل على 240 نطرح 5 نحصل على 235 نجعلها بدل 24 في 32.24 فيكون الحد الفعلي الأدنى = 32.235

 

(5) الجدول التالي يبين درجات إحدى المدارس القسم العلمي في الثانوية العامة حيث المجموع الكلي للدرجات 500

 

Total More than 450 400 ــ 350 ــ 300 ــ 250 ــ  200 ــ 150 ــ 100 ــ 50 ــ Less than 50 Interval  (X)
200 16 12 38 42 4 9 11 32 14 22 Frequency (F)

 

والمطلوب:

    1) الجدول التكراري المتجمع الصاعد والمتجمع الصاعد النسبي.

    2) عدد الطلاب الذين حصلوا على 70% ( 350 درجة) فأكثر.

    3) حدد عدد الناجحين باعتبار الحد الأدنى لدرجة النجاح 60% ( 300 درجة).

    4) حدد الدرجة التي لم يتجاوزها 40% من الطلاب.

    5) التمثيل البياني لكل من الجدول التكراري (Histogram) والمضلع التكراري (Polygon) والمنحى التكراري (Curve).

    6) التمثيل البياني لكل من والتكرار المتجمع الصاعد (CF) والتكرار المتجمع النسبي  (RCF).

الحـــل:

(1)

التكرار المتجمع الصاعد النسبي

Relative Cumulative Frequency (RCF)

التكرار المتجمع الصاعد

Cumulative Frequency (CF)

الفئات

  (X)

22 ÷ 200 = 0.11 22 Less than 50
0.18 36 Less than 100
0.34 68 Less than 150
0.40 79 Less than 200
0.44 88 Less than 250
0.46 92 Less than 300
0.67 134 Less than 350
0.86 172 Less than 400
0.92 184 Less than 450
1.00 200 More than 450

(2) عدد الطلاب الذين حصلوا على 70% ( 350 درجة) فأكثر = 66 طالب ( مقابل 350ــ في التكرار الصاعد 134 وباقي 200 هو 66 من 200 –  134 ) اللون الأصفر.

(3) عدد الناجحين باعتبار الحد الأدنى لدرجة النجاح 60% ( 300 درجة) = 108 حيث 60% أي 300 درجة يقابلها 134ما قبلها راسب (200 – 92) اللون الأزرق.

(4) الدرجة التي لم يتجاوزها 40% من الطلاب هي 200 ( اللون الخضر)

(5) ، (6)  التمثيل البياني

 

تنويه: من الممكن الحصول على النتائج ( لكل من 2 ، 3 ، 4 ) السابقة من الجدول الأصلي كالتالي:

 

Total More than 450 400 ــ 350 ــ 300 ــ 250 ــ  200 ــ 150 ــ 100 ــ 50 ــ Less than 50 Interval  (X)
200 16 12 38 42 4 9 11 32 14 22 Frequency (F)

 

(2) عدد الطلاب الذين حصلوا على 70% ( 350 درجة) فأكثر = 12 + 16 + 38 = 66 ( اللون الأصفر أعلاه).

(3) عدد الناجحين باعتبار الحد الأدنى لدرجة النجاح60% أي 0.60 × 500 أي 300 هو 42 + 38 + 12 + 16= 108 (مجموع الأعداد الأربعة الأخيرة في الجدول).

(4) الدرجة التي لم يتجاوزها 40% من الطلاب أي 0.40 × 200 = 80 طالب هي 200 ( نجمع من البداية حتى ≤ 80 أي 79 (اللون الأخضر) أي ما قبل 200 درجة.

 

(6) البيانات التالية هي درجات 50 طالب في مادة الإحصاء

27    33    45    40    33    37    28    29    40    41

32    37    35    38    37    39    40    42    46    48

33    37    38    40    28    26    32    36    36    44

42    43    45    29    28    27    35    34    36    37

45    41    38    37    28    28    29    33    34    35

    والمطلوب:

        تمثيل البيانات باستخدام طريقة الساق والورقة (Stem - and - Leaf).

        التمثيل البياني باستخدام برنامج MINITAB أو أي طريقة أخرى

 

 

الحـــل:

 2    │   6778888899                                (11)

 3    │  223333445556667777778889     (24)

 4    │  000011223455568                       (15)

                                                                 ـــــــــ

Total                                                          50 

يمكن استخدام برنامج SPSS كما يلي:

    ادخل البيات في العمود الأول وأعطي لها المتغير x

    انقر على Analyze ومنه انقر على Descriptive Statistics واختار Explore انقل المتغير x لخانة Dependent list وعلم أمام Plots ثم انقر على Plots واختار من القائمة Stem - and - Leaf ثم Continue ثم OK فنحصل على المطلوب وهذا توضيح لما ذكرناه

 

    كما يمكن استخدام برنامج MINITAB كما يلي:

    ادخل البيات في العمود الأول وأعطي لها المتغير X واتبع الخطوات المبينة بالشكل الآتي:

 

 

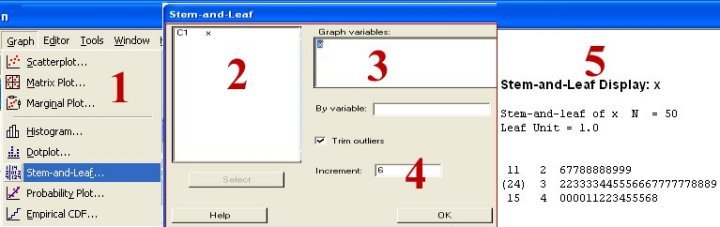
التمثيل البياني باستخدام MINITAB

 

(7) الجدول التكراري الآتي يبين درجات 45 طالب في مادة الإحصاء ( الدرجة النهائية 50) والمطلوب تكوين جدول يتضمن كل ما تعرفه من معلومات.

 

Interval 16 – 20 21 – 25 26 – 30 31 – 35 36 – 40 41 – 45 46 – 50
Frequency 1 2 9 12 10 8 3

 

الحـــل:

 

Interval Frequency Mid Interval Exact Lower Limits Exact Upper Limits CF RF RF%
16 – 20 1 18 15.5 20.5 1 0.02 2%
21 – 25 2 23 20.5 25.5 3 0.07 7%
26 – 30 9 28 25.5 30.5 12 0.27 27%
31 – 35 12 33 30.5 35.5 24 0.53 53%
36 – 40 10 38 35.5 40.5 34 0.76 76%
41 – 45 8 43 40.5 45.5 42 0.93 93%
46 – 50 3 48 45.5 50.5 45 1.00 100%
Total 45