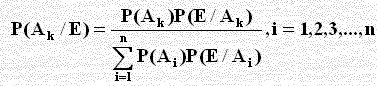
نظرية بييز Bayes theorem

إذا وقع الحدث E مع أحد الأحداث الشاملة A₁, A₂, A₃ , ..., A_n لفضاء عينة S و P(E) > 0   فإن:

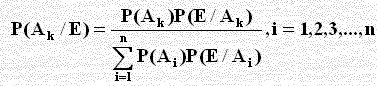
والنظرية هي أحدى طرق الاستدلال الرياضي حيث يكون لدينا مجتمع أو ظاهرة تتبع توزيع احتمالي معين معتمداً على معلمة ثابتة مجهولة ونريد الحصول على تقدير فترة للمعلمة هذه أو نختبر فرضاً معيناً من خلال بيانات لعينة عشوائية مأخوذة من هذا المجتمع حيث لدينا معلومات احتمالية قبلية (Prior probability) (قبل اخذ العينة) عن هذه المعلمة التي تأخذ قيماً مختلفة لتصبح متغير عشوائي له توزيع احتمالي نحصل عليه باستخدام هذه النظرية، والتوزيع الاحتمالي الناتج بعد أخذ العينة ويعرف بالتوزيع ألبعدي (Posterior distribution) وهو تلخيصاً للبيانات التي نحصل عليها من العينة بالإضافة للمعلومات القبلية مما يمكننا من تقدير هذه المعلمة المجهولة.

المثال التالي يوضح مفهوم هذه النظرية:

مثال(1)                    مثال(2)                    مثال(3)                    مثال(4)                    مثال(5)

    في بحث على طلبة كلية الطب في السنة النهائية في مادة التشريح وجدَّ أنَّ 20% من الطلبة والطالبات ممتازون وأنَّ 70% متوسطون وأنَّ الباقون ضعاف ووجدَّ أنَّ نسبة الطالبات في هذه المجموعات الثلاث هي 50%، 60%، 30% على الترتيب. فإذا اختير عشوائياً شخصاً من بينهم ووجدَّ أنه طالبة فاحسب احتمال أن تكون هذه الطالبة متوسطة في مادة التشريح.

الحــل:

    بفرض أن E حدث أن الشخص المختار عشوائياً طالبة (ممتازة) ، k = 2 فإنَّ:

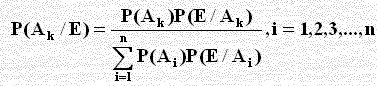
                                                 0.70 × 0.60

                        = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

                              0.20 × 0.50 + 0.70 × 0.60 + 0.10 × 0.30

                        = 0.7636

مثال (2)

    يوجد في مصنع ثلاث ماكينات تنتج الأولى 450 وحدة يومياً والثانية 350 وحدة يومياً والثالثة تنتج 200 وحدة يومياً وكانت نسبة المعيب من إنتاج الماكينة الأولى 1% ومن الثانية 2% ومن الثالثة 3% . اختيرت من إنتاج المصنع وحدة عشوائياً فوجدت أنها معيبة فاحسب احتمال أن تكون الوحدة المختارة من الماكينة الثانية.

الحــل:

    بفرض أن E حدث أن الوحدة المختارة عشوائياً معيبة ، k = 3 والوحدات المنتجة = 450 + 350 + 200 = 1000 وحدة

    نسبة إنتاج الماكينة الأولى هي (450÷1000) = 0.45

    نسبة إنتاج الماكينة الثانية هي (350÷1000) = 0.35

    نسبة إنتاج الماكينة الثالثة هي (200÷1000) = 0.20  فإنَّ:

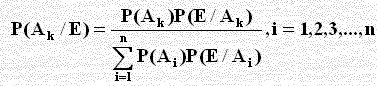
                                                 0.35 × 0.02

                        = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

                              0.45 × 0.01 + 0.35 × 0.02 + 0.20 × 0.03

                                         نضرب الحدود في 10000

                                     70

                        = ـــــــــــــــــــــــــــــــــــ

                              45 + 70 + 60

                        = 0.4

مثال (3)

            إذا ثلاث صناديق تحتوي على مصابيح كهربائية، الصندوق الأول به i40مصباحاً من بينها مصباحان معيبان والصندوق الثاني به i60مصباحاً من بينها i6مصابيح

            معيبة والصندوق الثالث به i80مصباحاً من بينها i12مصابيح معيبة. اختير احد المصابيح عشوائياً. احسب احتمال أن يكون معيباً وإذا كان معيب فما احتمال أن يكون

            من الصندوق الثالث.                ( الجواب i0.5) لاحظ ناتج مقام القانون وهو احتمال المعيب من الصناديق الثلاثة يساوي i0.10

الحـل:       

            احتمال اختيار صندوق من ثلاثة هو i 1/3

            احتمال المعيب من الصندوق الأول  هو i  2 / 40

            احتمال المعيب من الصندوق الثاني هو i  6 / 60 

            احتمال المعيب من الصندوق الثالث هو i 12 / 80 

            بفرض أن E حدث أن المصباح المختار عشوائياً معيب ، k = 3 فإنَّ:

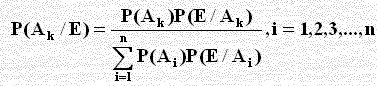
                                                (1/3) × (12/80)

                        = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

                              (1/3) × (2/40) + (1/3) × (6/60) + (1/3) × (12/80)

                                     0.05

                        = ـــــــــــــــــــــــــــــــــــــــــ

                             0.02 + 0.03 + 0.05

                             0.05

                        = ــــــــــــــ

                             0.10

                        = 0.05

مثال (4)

            تقدم طلاب ثلاثة مدارس لامتحان مادة الإحصاء في السنة النهائية، وكان عدد المتقدمين من المدرسة الأولى i60طالباً ومن الثانية i90طالباً ومن الثالثة i100طالباً

           وكانت نسبة النجاح في المدرسة الأولى i70%وفي الثانية i60%وفي الثالثة i50%. فإذا اختير طالباً عشوائياً من بين هؤلاء الطلاب ووجد ناجحاً فما احتمال أن

           يكون من المدرسة الثانية.        ( الجواب i0.34 )  لاحظ ناتج مقام القانون وهو احتمال النجاح هو i0.71

الحـل: 

            مجموع طلاب المدارس الثلاثة هو i 250     

            احتمال الطالب من المدرسة الأولى هو i250/60

            احتمال الطالب من المدرسة الثانية هو i 250/90

            احتمال الطالب من المدرسة الثالثة هو i 250/100 

            بفرض أن E حدث أن الطالب المختار عشوائياً ناجحا ، k = 3 فإنَّ:

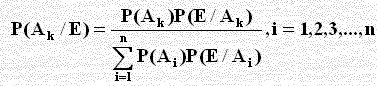
                                                (90/250) × 0.60

                        = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

                           (60/250) × 0.70 + (90/250) × 0.60 + (100/250) × 0.50

                                     0.22

                        = ـــــــــــــــــــــــــــــــــــــــــ

                             0.17 + 0.22 + 0.20

                             0.22

                        = ــــــــــــــ

                             0.59

                        = 0.37

مثال (5)

تشكلت لجنة من i18عضواً لتمثل الصفوف الأربعة في إحدى الكليات كالآتي:

            i3 أعضاء من الصف الأول منهم طالبة

            i5 أعضاء من الصف الثاني منهم طالبتان

            i6 أعضاء من الصف الثالث منهم ثلاثة طالبات

            i4 أعضاء من الصف الرابع منهم طالبتان

    اختير عضواً من هذه اللجنة عشوائياً ووجدَّ أنه طالبة فما احتمال أن تكون هذه الطالبة من الصف الثالث؟        (الجوابi0.25i )

الحـل:       

            مجموع الأعضاء i18 فاحتمال اختيار عضو من الصف الأول هو i3/18 ومن الصف الثاني i5/18 ومن الثالث i6/18 ومن الرابع i4/18

            بفرض أن E حدث أن المصباح المختار عشوائياً معيب ، k = 4 فإنَّ:

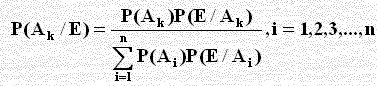
                                                                      (6/18) × (3/6)

                        = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

                              (3/18) × (1/3) + (5/18) × (2/5) + (6/18) × (3/6) + (4/18) × (2/4)

                                              0.17

                        = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

                             0.06 + 0.12 + 0.17 + 0.12

                             0.17

                        = ــــــــــــــ

                             0.47

                        = 0.36