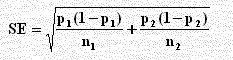
الاستدلال حول الفرق بين نسبتين:

    يوجد الكثير من التطبيقات التربوية نحتاج فيها للمقارنة بين مجتمعين من حيث نسبة عناصر تنتمي لصنفين في المجتمع كنسبة الطلاب الراغبون بدراسة مادة معينة إن كانت مساوية لنسبة الطالبات لنفس المادة لذا نأخذ عينة كبيرة من كل مجتمع فعمليات الاستدلال تعتمد على الفرق بين النسبتين فلذا فنحن في حاجة للتعرف على هذا الإحصاء.

توزيع المعاينة للفرق بين نسبتين:

    النسبتان في العينتين هما p₁ˆ و p₂ˆ مكبر حجمي العينتين n₁ , n₂ يكون توزيع الفرق بين المتوسطين (p₂ˆ ــ p₁ˆ) وهو يتبع توزيع طبيعي بمتوسط  (p₂ ــ p₁) وانحراف معياري.

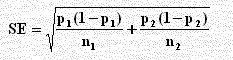
تقدير الفرق بين نسبتين:

تقدير النقطة للفرق بين النسبتين p₂ ــ p₁ هو الفرق بين النسبتين في العينتين أما تقدير الفترة نحصل عليه من الصيغة الرياضية

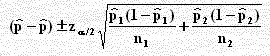
اختبار المقارنة بين نسبتين

    يهدف الاختبار للمقارنة بين النسبتين P₁ , P₂ أي اختبار فرض العدم H_o : P₁ = P₂ مقابل أحد الفروض البديلة وهي:

H₁ : P₁ > P₂ أو H₁ : P₁ < P₂ أو H₁ : P₁ ≠ P₂ ومن حيث نعتبر H_o صحيحة أي p = p₁ = p₂ فيكون SE كالآتي:

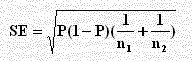
وتبقى هذه النسبة مجهولة فنحتاج لتقديرها وأفضل تقدير لها النسبة المشتركة للعينتين أي:

توزيع إحصاء الاختبار بعد تعويض P بتقديرها P^ˆ هو طبيعي معياري بشرط كبر حجم العينة.