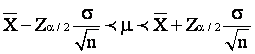
إذا كان الوسط الحسابي لأوزان 25 فرداً لعينة عشوائية يساوي 63 والانحراف المعياري لها يساوي 12. أوجد فترة ثقة للمتوسط بدرجة ثقة 99%، وإذا استخدمت عينة عشوائية مكونة من 400 فرد فأوجد فترة الثقة وقارنها مع الفترة السابقة.

الحــل:

 الانحراف المعياري للمجتمع معلوم ويساوي 12

                                ــــ

Z α/2 = 2.58, σ =12, X = 63, n = 25

    وبتطبيق الصيغة الرياضية

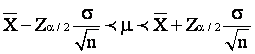
63 - 2.58(12/5)< μ < 63 + 2.58 (12/5)

63 - 6.192< μ < 63 +6.192

56.808 < μ < 69.192

وعليه يتراوح متوسط مجتمع الأوزان من 56.808 إلى 69.192 بثقة 99%

العينة الجديدة حجمها 400

Z α/2 = 2.58, σ =12, X = 63 , n = 400

    وبتطبيق الصيغة الرياضية

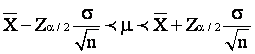
63 - 2.58(12/20)< μ < 63 + 2.58 (12/20)

63 - 1.548< μ < 63 +1.548

61.452 < μ < 64.548

وعليه يتراوح متوسط مجتمع علامات الأوزان من 61.452 إلى 64.548 بثقة 99%

الملاحظة:

في الفترة الأولى المدى 69.192 – 56.808 = 12.384

في الفترة الثانية المدى 64.548 – 61.452 = 3.096 أقل عنها من السابقة

لاحظ أن الحد الأدنى للفترة زادت قيمته واقترب أكثر من المتوسط الحسابي (63)

لاحظ أن الحد الأعلى للفترة قلت قيمته واقترب أكثر من المتوسط الحسابي (63)

فيما يلي أخذنا حجم للعينة أكبر 900 ، 2500 ونجد الفارق الواضح كلما كبر حجم العينة كلما اقتربت حدود فترة الثقة من الوسط الحسابي للعينة.

العينة الجديدة حجمها 900

Z α/2 = 2.58, σ =12, X = 63 , n = 900

    وبتطبيق الصيغة الرياضية

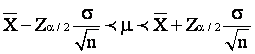
63 - 2.58(12/30)< μ < 63 + 2.58 (12/30)

63 - 1.032< μ < 63 +1.032

61.968 < μ < 64.032

العينة الجديدة حجمها 2500

Z α/2 = 2.58, σ =12, X = 63 , n = 2500

    وبتطبيق الصيغة الرياضية

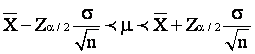
63 - 2.58(12/50)< μ < 63 + 2.58 (12/50)

63 - 0.619< μ < 63 +0.619

62.381 < μ < 63.619