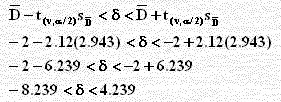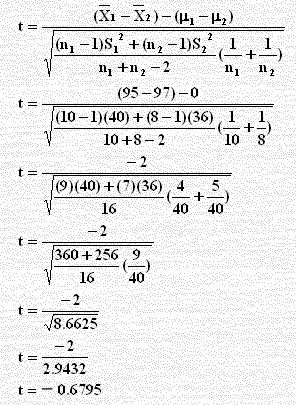
مثال 4:
باحث تربوي أراد تقييم قدرة الطفل على تعلم كلمات جديدة ومدى اختلاف ذلك باختلاف الجنسية بافتراض أن درجات اختبار الطفل على تعلم اللغة يتبع توزيعين معتدلين لهما نفس التباين، وأعطى الاختبار لمجموعتين عشوائيتين مستقلتين من الأطفال عمر خمسة سنوات فحصلنا على الآتي:
| المجموعة الثانية | المجموعة الأولى |
| n2 = 8 | n1 = 10 |
|
ــــ X = 97 |
ــــ X = 95 |
| S12 = 36 | S22 = 40 |
1) استخدم α = 0.05 لاختبار الفرض القائل بتساوي قدرات أطفال المجموعتين على تعلم كلمات جديدة.
2) أوجد فترة ثقة 95% للفرق الحقيقي.
الحــل:ـ
أولا: 1)
ليكن μ1 متوسط تعلم الطفل كلمات جديدة في المجموعة الأولى ،
μ2 متوسط تعلم الطفل كلمات جديدة في المجموعة الثانية، ويكون فرضي العدم والبديل:
Ho : μ1 = μ2 , H1 : μ1 ≠ μ2
واضح أن الاختبار ذو طرفين وعليه يمكن رفض Ho الوسط الأول أقل أو أكبر بدرجة معنوية من الوسط الثاني وقيمتي t الحرجتان هما ± 2.12 عند 0.05 هي وقاعدة القرار هي:
رفض Ho عندما: t ≤ – 2.12 أو t ≥ 2.12
نستخدم الصيغة الرياضية أعلاه للحصول على قيمة Z:
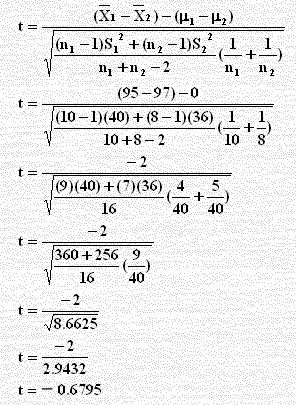
قيمة t = – 0.68 أكبر من قيمة α = – 2.12 الجدولية فنقبل Ho عند مستوى دلالة 0.05 والشكل التالي يبين ذلك
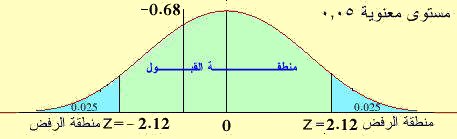
ثانياً: 2)
مما سبق وجدنا D`تساوي –2 (فرق المتوسطين) ، t(v, α/2) = t(16, 0.025) = ±2.12 , S`D = 2.943 يمكن الحصول على فترة ثقة 95% كالآتي: