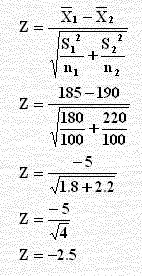
مثال 3:
البيانات التالية تبين نتائج تغذية مجموعتين من الماشية بنوعين مختلفين من الغذاء
| الغذاء الثاني | الغذاء الأول | |
| n2 = 100 | n1 = 100 | عدد الماشية |
|
ــــ X = 190 |
ــــ X = 185 |
متوسط الزيادة في الوزن |
| S12 = 220 | S22 = 180 | تباين العينة |
بفرض تشابه جميع العوامل الأخرى المؤثرة في الوزن اختبر تساوي تأثير نوعي الغذاء على الوزن مقابل الاختلاف عند مستوى دلالة 0.05
ليكن μ1 متوسط الزيادة في النوع الأول ، μ2 متوسط الزيادة في النوع الثاني ويكون فرضي العدم والبديل:
Ho : μ1 = μ2 , H1 : μ1 ≠ μ2
واضح أن الاختبار ذو طرفين وعليه يمكن رفض Ho الوسط الأول أقل أو أكبر بدرجة معنوية من الوسط الثاني والقيمة الحرجة عند 0.05 هي 1.96 وقاعدة القرار هي:
رفض Ho عندما: Z ≤ – 1.96 أو Z ≥ 1.96
نستخدم الصيغة الرياضية أعلاه للحصول على قيمة Z:
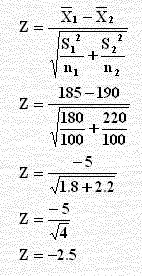
قيمة Z أقل من – 1.96 فنرفض Ho عند مستوى دلالة 0.05 والشكل التالي يبين ذلك
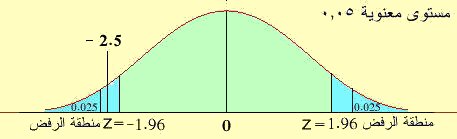
تمرين: أعد الحل عند مستوى معنوية α = 0.01 والإجابة بقبول Ho فرض العدم