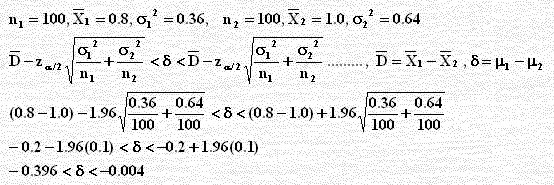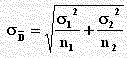
مقدّر فترة ثقة للفرق بين متوسطي مجتمعين:
الهدف اختبار ما كان الفرق بين المتوسطين يعزى للصدفة (الفرق صغير) أو أنه اختلاف جوهري (الفرق كبير) يعني بالقول بأنهما من مجتمعين مختلفين، فمثلاً كسحب عينة من الرجال يقومون بإنتاج مادة ما فوجد متوسط الإنتاج 50 في حين سحبت عينة من النساء ولنفس العمل فوجد المتوسط لهن هو 63 فهل الفارق هنا يرجع للصدفة أو أنه حقيقي في أداء الجنسين وكمثال آخر كرغبتنا في مقارنة متوسط درجات طلاب في مجتمعين مختلفين.
ـــ ـــ ـــ
اختبار الفرق بين متوسطين D = X1–X2 حيث X1 هو متوسط عينة عشوائية من مجتمع متوسطه μ1 ، وأن X2 متوسط عينة
عشوائية من مجتمع متوسطه μ2 ، وتوزيع المعاينة للمتغير D` له معلمتين هما الوسط الحسابي والانحراف المعياري فوسطه
الحسابي δ (دلتا) ويساوي μ1 – μ2 في حين يحسب الانحراف المعياري للمتغير D` من القانون التالي الذي يحسب الخطأ المعياري للفرق بين المتوسطين لعينتين مستقلتين، حيث σ2 تباين المجتمع ويرقم ب 1 للمجتمع الأول ( مفردات العينة منه n1 ) و 2 للمجتمع الثاني ( مفردات العينة منه n2 ).
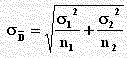
وفي حال كبر حجم العينتين فإن D` تتوزع توزيعاً معتدلاً متوسطه μ1 – μ2 في حين تباينه القيمة تحت الجذر ألتربيعي أعلاه وبصرف النظر عن شكل التوزيعين الأصليين. تحسب فترة الثقة هنا كما سبق في حالة المجتمع الواحد مع الفارق هنا في حساب الفرق بين متوسطي المجتمعين وعليه تكون فترة الثقة (1– α ) للفرق بين متوسطي المجتمعين هي:
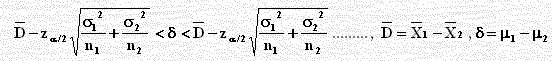
مثال:
لتقدير الفرق بين كمية النيكوتين في نوعين من السجائر، أخذت عينة عشوائية من مجتمع وكان حجمها 100، وكان متوسطها الحسابي 0.8 وكان تباين المجتمع 0.36 وأخذت عينة عشوائية من مجتمع آخر وكان حجمها 100، وكان متوسطها الحسابي 1.0 وكان تباين المجتمع 0.64 والمطلوب فترة ثقة 0.95 بين متوسط كمية النيكوتين في النوعين.
الحل:
بتطبيق الصيغة السابقة: