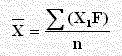
(1) من الجدول التكراري الآتي:
|
Total |
18 | 16 | 14 | 12 | 10 | 8 | 6 | 4 | 2 | Interval |
| 64 | 5 | 6 | 7 | 9 | 11 | 9 | 7 | 6 | 4 | Frequency |
أوجد قيمة الوسط الحسابي بطرقه المختلفة.
الحـل:
لاحظ: في البيانات المبوبة قانون الوسط الحسابي هو: X = (∑xi fi) / ∑fi`وللوسط الفرضي: X0 = (∑Di fi) / ∑fi`حيث أن: i = 1 , 2 , ... , n ، ∑fi = n
نكون الجدول الآتي:
| X1 × F | Mid Interval (X1) | Frequency (F) | Interval (X) |
| 12 | 3 | 4 | 2 – |
| 30 | 5 | 6 | 4 – |
| 49 | 7 | 7 | 6 – |
| 81 | 9 | 9 | 8 – |
| 121 | 11 | 11 | 10 – |
| 117 | 13 | 9 | 12 – |
| 105 | 15 | 7 | 14 – |
| 102 | 17 | 6 | 16 – |
| 95 | 19 | 5 | 18 – |
| 712 | 64 | Total |
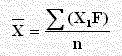
Mean = 712 / 64
= 11.125
باستخدام الوسط الفرضي (Fictitious Mean):
| X2 × F | Deviations (X2) | Mid Interval (X1) | Frequency (F) | Interval (X) |
| – 32 | – 8 | 3 | 4 | 2 – |
| – 36 | – 6 | 5 | 6 | 4 – |
| – 28 | – 4 | 7 | 7 | 6 – |
| – 18 | – 2 | 9 | 9 | 8 – |
| 0 | 0 | 11 | 11 | 10 – |
| 18 | 2 | 13 | 9 | 12 – |
| 28 | 4 | 15 | 7 | 14 – |
| 36 | 6 | 17 | 6 | 16 – |
| 40 | 8 | 19 | 5 | 18 – |
| 8 | 0 | 64 | Total |
نختار X0=11 كوسط فرضي.
![]()
Mean = 11 + 8 / 64
= 11 + 0.1257
= 11.125
باستخدام الطريقة المختصرة:
بإضافة عمود جديد بقسمة الانحرافات على طول الفئة:
| (X2 / 2) × F | X2 / 2 | Deviations (X2) | Mid Interval (X1) | Frequency (F) | Interval (X) |
| – 16 | – 4 | – 8 | 3 | 4 | 2 – |
| – 18 | – 3 | – 6 | 5 | 6 | 4 – |
| – 14 | – 2 | – 4 | 7 | 7 | 6 – |
| – 9 | – 1 | – 2 | 9 | 9 | 8 – |
| 0 | 0 | 0 | 11 | 11 | 10 – |
| 9 | 1 | 2 | 13 | 9 | 12 – |
| 14 | 2 | 4 | 15 | 7 | 14 – |
| 18 | 3 | 6 | 17 | 6 | 16 – |
| 20 | 4 | 8 | 19 | 5 | 18 – |
| 4 | 0 | 0 | 64 | Total |
![]()
Mean = 11 + (4 / 64) × 2
= 11 + 0.125
= 11.125