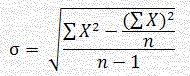
(1) أذكر علاقة الانحراف المعياري بالتباين.
قيمة الانحراف المعياري ( σ للعينة أو μ للمجتمع ) تساوي الجذر ألتربيعي للتباين ( S2 ).
(2) احسب التباين والانحراف المعياري للقيم: i3 ، 5 ، 7 ، 11 ، 13 ، 18 ، 20
نحسب الوسط الحسابي لمجموعة القيم بجمعها ومن ثم قسمتها على عددها أي: i( 3 + 5 + 7 + 11 + 13 + 18 + 20) ÷ 7 = 77 ÷ 7 = 11
نحسب فروق القيم عن وسطها وهي: i 3 – 11 ، 5 – 11 ، 7 – 11 ، 11 – 11 ، 13 – 11 ، 18 – 11 ، 20 – 11 (الانحرافات عن المتوسط الحسابي).
i– 8 ، – 6 ، – 4 ، 0 ، 2 ، 7 ، 9
نربع الفروق في الخطوة السابقة أي i 64 ، 36 ، 16 ، 0 ، 4 ، 49 ، 81
نجمع مربعات الفروق السابقة أي: i 64 + 36 + 16 + 0 + 4 + 49 + 81 = 250
نحسب متوسط مربعات الفروق (التباين) =i250 ÷ 7 = 35.7143 كمجتمع ، i 250 ÷ 6 = 41.6667 كعينة
نحسب الجذر ألتربيعي للمتوسط في الخطوة السابقة وهو الانحراف المعياري أي μ = 5.9761 للمجتمع , σ = 6.4550 للعينة
(3) أذكر العلاقة الرياضية لحساب الانحراف المعياري ومنها احسب الانحراف المعياري للقيم في السؤال السابق.
العلاقة الرياضية للانحراف المعياري(σ) للعينة هي:
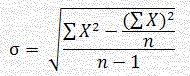
لحساب الانحراف المعياري نحسب مجموع مربعات القيم أي:i 9 + 25 + 49 + 121+ 169 + 324 + 400 = 1097 حيث أنَّ مجموع القيم = i77 أي:
∑ X = 77 , (∑ X)2 = 1097
وبتطبيق العلاقة السابقة نجد أنَّ:

وهي نفس النتيجة السابقة مع ملاحظ أن التباين = i41.6667
(4) أذكر قانون حساب الانحراف المعياري للبيانات المبوبة ثم احسب الانحراف المعياري لدرجات 30 طالب مبينة في الجدول الآتي:
| Total | 21 – 23 | 18 – 20 | 15 – 17 | 12 – 14 | 9 – 11 | 6 – 8 | 3 – 5 | Interval |
| 30 | 1 | 3 | 4 | 8 | 6 | 5 | 3 | Frequency |
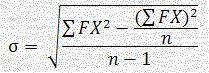
نكون الجدول التالي:
| FX2 | X2 | FX | Mid Interval (X) | Frequency (F) | Interval |
| 48 | 16 | 12 | 4 | 3 | 3 – 5 |
| 245 | 49 | 35 | 7 | 5 | 6 – 8 |
| 600 | 100 | 60 | 10 | 6 | 9 – 11 |
| 1352 | 169 | 104 | 13 | 8 | 12 – 14 |
| 1024 | 256 | 64 | 16 | 4 | 15 – 17 |
| 1083 | 361 | 57 | 19 | 3 | 18 – 20 |
| 484 | 484 | 22 | 22 | 1 | 21 – 23 |
| 4836 | 356 | 30 | Total |
نطبق القانون الرياضي السابق:

يلاحظ أن التباين يساوي S2 =i22.717 كما يلاحظ أنَّ S هو الانحراف المعياري (σ)
(5) أكتب الصيغة الرياضية لحساب تباين لمجتمع يتألف من عدة عينات.
وإذا كان لدينا مجتمع مكون من العينة i 3 ، 5 ، 4 ، 6 ، 7 ، 6 ، 4 والعينة i 6 ، 7 ، 4 ، 5 ، 3 فاحسب مقدار تباين المجتمع.
(n1 – 1)S12 + (n2 – 1)S22 + ... + (nk – 1)Sk2 + n1(`X1 –`X ) + n2(`X2 –`X ) + ... + nk(`Xk –`X )
S2 = ————————————————————————————————————————
n1 + n2 + ... + nk – 1
حيث X`الوسط المرجح (الموزون) لمجتمعين وقد سبق ذكره في الوسط الحسابي والتباين لمجموعتين أو عينتين يوجد من الصيغة الرياضية:
(n1 – 1)S12 + (n2 – 1)S22 + n1(`X1 –`X ) + n2(`X2 –`X )
S2 = ————————————————————————
n1 + n2 – 1
نحسب الوسط الحسابي لكل عينة وكذلك للعينتين معاً ثم نحسب التباين لكل منهم ومن ثم التباين العام
|
العينة الأولى `X1 = (3+5+4+6+7+6+4) ÷ 7 = 5 S12 = [(3–5)2 +(5–5)2 +(4–5)2 +(6–5)2 +(7–5)2 +(6–5)2 +(4–5)2] ÷ (7–1) S12 = (4+0+1+1+4+1+1) ÷ 6 S12= 2 |
العينة الثانية `X2 = (2+1+4+5+3) ÷5 = 3 S22 = [(2–3)2 +(1–3)2 +(4–3)2 +(5–3)2 +(3–3)2 ÷(5–1) S22 = (1+4+1+4+0) ÷ 4 S22 = 2.5 |
نحسب الوسط المرجح:
n1`X1 + n2`X2
`X = ————————
n1 + n2
7×5 + 5×3
`X = ————— = 4.17
7 + 5
نحسب التباين العام للعينات(للعينتين):
(n1 – 1)S12 + (n2 – 1)S22 + n1(`X1 –`X ) + n2(`X2 –`X )
S2 = ————————————————————————
n1 + n2 – 1
(7 – 1)×2 + (5 – 1)×2.5 + 7(5 – 4.17 ) + 5(3 – 4.17 )
S2 = ————————————————————————
7 + 5 – 1
12 + 10 +5.81 – 5.85
S2 = ————————— ≈ 2
11
(6) ما هو معامل الاختلاف؟ وفيما يستخدم؟ وأعطي مثلاً لذلك.
يعرف معامل الاختلاف لتوزيع حسب الصيغة الرياضية V = ( σ ÷`X) ×100 حيث V معامل الاختلاف ، σ الانحراف المعياري ، X`الوسط الحسابي.
وهو نوعان، كمي (للمتغيرات الكمية وقانونه V = ( σ ÷`X) ×100 ) ونوعي (للمتغيرات النوعية كالجنس وقانونه V = k(n2–∑X2) / n2(k–1)i حيث k عدد
مستويات المتغير الاسمي، n عدد أفراد العينة، X عدد الأفراد في كل مستوى من مستويات المتغير الاسمي ومعامل الاختلاف مقياس للتشتت في إحدى حالتين:
1) اختلاف المتوسطات كبير كمقارنة تشتت أوزان الفيلة مع أوزان القطط.
2) في اختلاف وحدات القياس كتشتت أطوال مجتمع مع أوزان المجتمع نفسه.
مثال ذلك: المتوسط الحسابي لأوزان طلبة فصل دراسي هو i65كيلوجرام بانحراف معياري قدره i6فإن V = (6 ÷ 65) × 100 = 9.23حسب العلاقة الرياضية السابقة.
حال المقارنة بين تشتت مجموعتين نحسب معامل الاختلاف لكل منهما والأكبر يكون للمجموعة الأكثر تشتتاً.
مثال آخر: الجدول التالي يبين توزيع الطلاب الأجانب حسب جنسياتهم في كليتي الهندسة والعلوم بإحدى الجامعات الأمريكية، احسب معامل الاختلاف النوعي.
| المجموع | عراقي | سوداني | لبناني | سوري | أردني | فلسطيني | مصري | الجنسية |
| 75 | 6 | 13 | 9 | 12 | 7 | 8 | 20 | كلية الهندسة (X) |
| 80 | 5 | 10 | 8 | 15 | 8 | 12 | 22 | كلية العلوم (X) |
لكلية الهندسة: عدد مستويات المتغير الاسمي k = 7 (الجنسيات) وعدد أفراد العينة n = 75
∑X2 = 400+64+49+144+81+169+36 = 943
k(n2–∑X2) 7(752 – 943) 32774
V = ————— = —————— = ———— = 0.971
n2(k–1)i 752(7 – 1) 33750
لكلية العلوم عدد مستويات المتغير الاسمي k = 8 (الجنسيات) وعدد أفراد العينة n = 80
∑X2 = 484+144+64+225+64+100+25 = 1106
k(n2–∑X2) 7(802 – 1106) 37058
V = ————— = —————— = ———— = 0.965
n2(k–1)i 802(7 – 1) 38400
معامل اختلاف طلبة الهندسة أكبر من معامل اختلاف طلبة العلوم لذا توزيع الطلاب على كلية الهندسة أكثر تشتتاً.
(7) هل تتأثر قيم مقاييس التشتت بالعمليات الحسابية؟
المدى والتباين والانحراف المعياري لا تتأثر بعمليات الجمع والطرح (يتأثر المتوسط) ولكن تتأثر في الضرب والقسمة بالكمية المضروبة (المطلقة) أو المقسومة (المطلقة) وعليه يمكن عند حساب الانحراف المعياري مثلاً لقيم كبيرة نقوم بطرح القيمة الأصغر من كل القيم فيسهل حساب مجموعها ومجموع مربعاتها والانحراف المعياري الناتج لا تختلف قيمته عن حسابه للقيم الأصلية.
توضيح:
الانحراف المعياري لدرجات اختبار i6 فإذا ضربنا كل درجة في i 2 أو i –2 فإن الانحراف المعياري الجديد = i6 ×|±2| = 6 × 2 = 12حيث | | رمز القيمة المطلقة.
والتفسير الرياضي لذلك لمجموعة من القيم متوسطها X`وبضرب كل قيمة بثابت C يكون الوسط الحسابي الجديد هوXC`ويكون الانحراف عن المتوسط بعد عملية الضرب هذه هو CX ــ XC`ويكون التباين:
S2 = ∑ ( CX –`XC )2 ÷ (n – 1)
= C2 ∑(X –`X )2 ÷ (n – 1)
= C2 σ2
الانحراف المعياري الجديد = C σ
وهو الثابت C مضروب في الانحراف المعياري الأصلي
لكن الإضافة لكل درجة يعني إزاحة التوزيع جهة اليمن إن كانت موجبة وجهة اليسار إن كانت سالبة على الخط الأفقي دون تغير في شكل التوزيع

والضرب في ثابت موجب فيعني إزاحة المتوسط لليمين ويمتد النصف الأعلى للتوزيع أكثر من نصفه الأسفل ويصبح المنحنى ملتو التواء موجب

والضرب في ثابت سالب فيعني إزاحة المتوسط لليسار ويتقلص النصف الأعلى للتوزيع أكثر من نصفه الأسفل ويصبح المنحنى ملتو التواء سالب
