تقدم i10طلاب لاختبارين في الرياضيات والعلوم مبينة درجاتهم في الجدول التالي:
| 46 | 41 | 40 | 40 | 39 | 39 | 36 | 35 | 34 | 30 | Math. (X) |
| 81 | 80 | 83 | 76 | 79 | 73 | 80 | 76 | 70 | 72 | sciences (Y) |
احسب معامل الارتباط لعلامات الطلاب ( rxy ) وكذلك معادلة الانحدار
الحــل:
القوانين المستخدمة هنا هي: S2 = [ ∑ (xi –`X )2] / n حيث S الانحراف المعياري أو σ ، كما أنَّ S2 مقدار التباين
Zx = (X –`X) ÷ Sx ، Zy = (Y–`Y ) ÷ Sy ، rxy = [∑( Zx Zy)] / n
لحساب معامل الارتباط نكون الجدول التالي:
| Zx Zy | Zy | (Y –`Y)2 | Y –`Y | Zx | (X –`X)2 | X –`X | Y | X |
| 2.340 | – 1.227 | 25.000 | – 5.000 | – 1.907 | 64.000 | – 8.000 | 72 | 30 |
| 1.638 | – 1.718 | 49.000 | – 7.000 | – 0.954 | 16.000 | – 4.000 | 70 | 34 |
| 0.176 | – 0.245 | 1.000 | – 1.000 | – 0.715 | 9.000 | – 3.000 | 76 | 35 |
| – 0.351 | 0.736 | 9.000 | 3.000 | – 0.477 | 4.000 | – 2.000 | 80 | 36 |
| – 0.234 | – 0.982 | 16.000 | – 4.000 | 0.238 | 1.000 | 1.000 | 73 | 39 |
| 0.117 | 0.491 | 4.000 | 2.000 | 0.238 | 1.000 | 1.000 | 79 | 39 |
| – 0.117 | – 0.245 | 1.000 | – 1.000 | 0.477 | 4.000 | 2.000 | 76 | 40 |
| 0.702 | 1.473 | 36.000 | 6.000 | 0.477 | 4.000 | 2.000 | 83 | 40 |
| 0.527 | 0.736 | 9.000 | 3.000 | 0.715 | 9.000 | 3.000 | 80 | 41 |
| 1.872 | 0.982 | 16.000 | 4.000 | 1.907 | 64.000 | 8.000 | 81 | 46 |
| 6.670 | 0.000 | 166.000 | 0.000 | 0.000 | 176.000 | 0.000 | 770 | 380 |
|
rxy = 6.670÷10 = 0.667 |
|
S2= 166/10 = 16.6 Sy = 4.047 |
|
|
S2= 176/10 = 17.6 Sx =4.195 |
|
`Y = 770/10 = 77 |
`Y = 380/10 =38 |
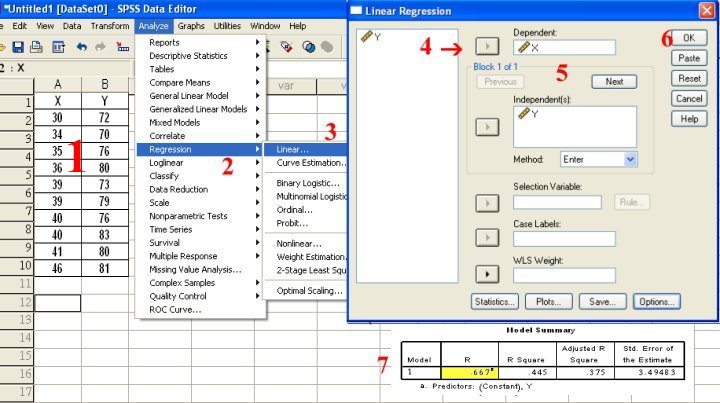
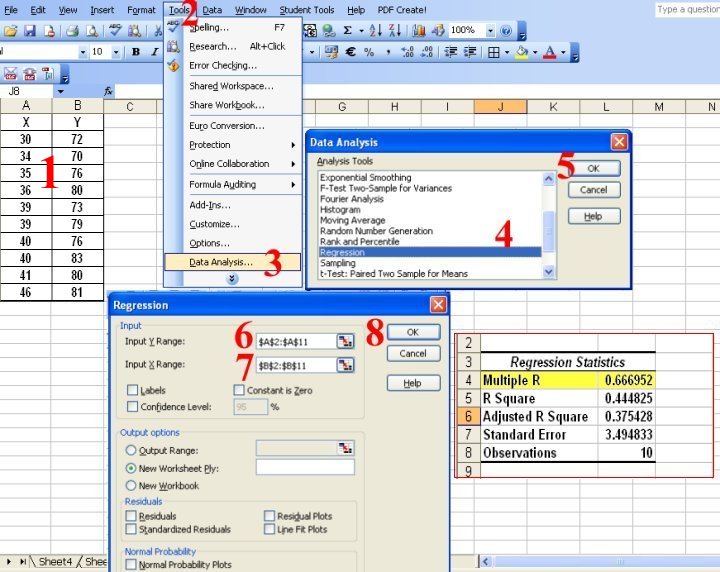
يمكن حساب معامل الارتباط بطرق أخرى وأهمها الحاسب الآلي وبرنامج SPSS أو EXCEL أو MINITAB و MINITAB لمعادلة الانحدار
نحسب كل من α و β من معادلة الانحدار Y = β X + α حيث β ميل الانحدار ، α ثابت الانحدار
βyx = rxy× (Sy / Sx) = 0.667 × (4.047 / 4.195 ) = 0.644
αyx =`Y – βyx`X = 77 – 0.644 × 38 = 52.528
معادلة الانحدار هي:
Y = 0.644 X + 52.528
من المعادلة السابقة نجد أن علامة الطالب في الإحصاء تزداد بمقدار i0.644لكل علامة واحدة زيادة في الرياضيات في حين لا تتغير قيمة العلامة في الإحصاء i52.528 كما يمكن معرفة علامة الإحصاء بالتعويض عن علامة الرياضيات في معادلة الانحدار باستبدال القيمة بالمتغير X في معادلة الانحدار فقيمة علامة الإحصاء عندما تكون علامة الرياضيات i35 مثلاً والقيمة الناتجة قد تختلف عن القيمة في جدول البيانات ( i35 التي تقابل i76) حال وجودها لكون العلاقة غير تامة والفرق بين القيمتين يعرف بخطأ التنبؤ أو خطأ التقدير ويرمز له بالرمز e ويكبر الفرق كلما ضعفت العلاقة ويقل كلما قويت العلاقة.
Y = 0.675 X + 27.425
Y' = 0.644 × 35 + 52.528 = 75.07
e = 76 – 75.07 = 0.93

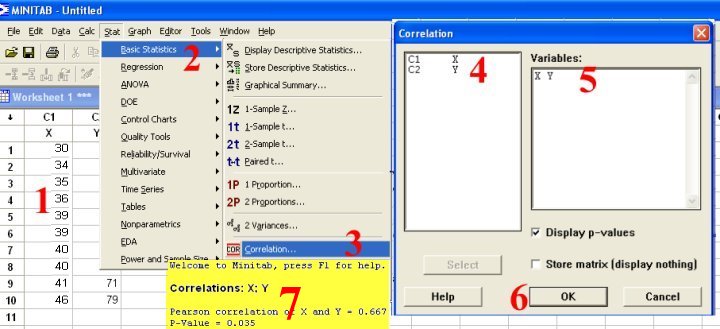
الحل باستخدام MINITAB لحساب معامل الارتباط
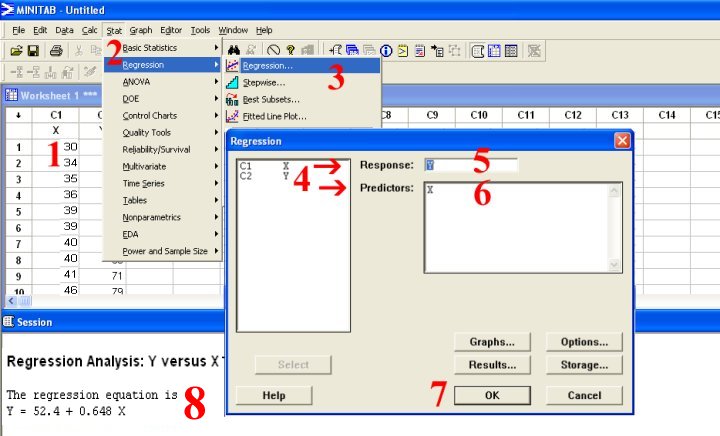
الحل باستخدام MINITAB لإيجاد معادلة الانحدار