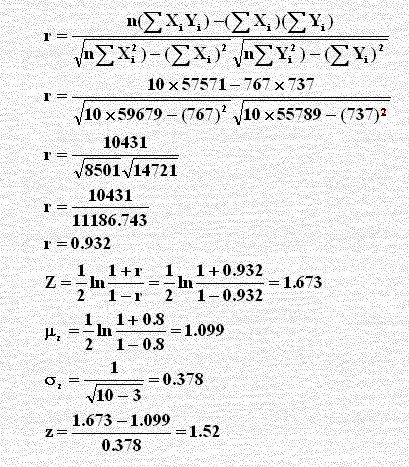
الحل:
| 74 | 92 | 88 | 65 | 71 | 88 | 66 | 70 | 80 | 73 | معدل الطالب في الصف |
| 72 | 88 | 90 | 55 | 64 | 92 | 70 | 64 | 78 | 64 | مدل الطالب في المدرسة |
نكون جدول لحساب معامل الارتباط بيرسون r
| X | Y | X Y | X2 | Y2 |
| 73 | 64 | 4672 | 5329 | 4096 |
| 80 | 78 | 6240 | 6400 | 6084 |
| 70 | 64 | 4480 | 4900 | 4096 |
| 66 | 70 | 4620 | 4356 | 4900 |
| 88 | 92 | 8096 | 7744 | 8464 |
| 71 | 64 | 4544 | 5041 | 4096 |
| 65 | 55 | 3575 | 4225 | 3025 |
| 88 | 90 | 7920 | 7744 | 8100 |
| 92 | 88 | 8096 | 8464 | 7744 |
| 74 | 72 | 5328 | 5476 | 5184 |
| 767 | 737 | 57571 | 59679 | 55789 |
نستعمل النظرية لحساب Z عند r =0.932 المحسوبة أدناه وكذلك حساب كل من μz , σz , z كالآتي:
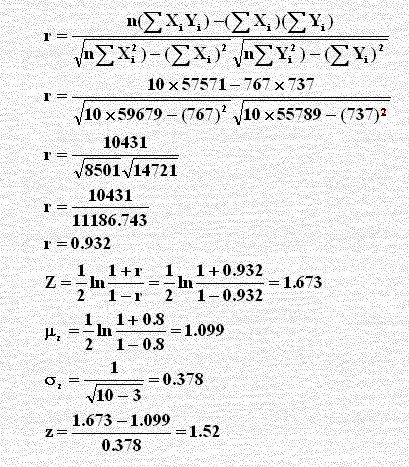
Z1–α/2=Z0.975=1.96 وحيث أن 1.41 < 1.96 نرفض Ho ونعتبر أن ρ ≠ 0.8
ولحساب فترة الثقة نجد r=0.966 تقابل Z = 2.029 وأن Z0.975=1.96 وبالتعويض في:
(Z + z1-α/2.σz , Z – z1-α/2.σz) أي
(2.029 – 1.96× 0.408, 2.029 + 1.96 × 0.408)
( 1.229 , 2.829) هي فترة ثقة (μz) يقابلها من جدول تحويل r إلى Z القيمتان (0.84 , 0.993) وهي فترة ثقة (ρ)