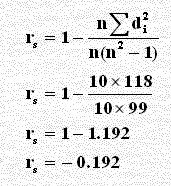
مثال:
اختيرت عينة عشوائية مكونة من 10 طلاب في لعبتي كرة اليد وكرة القدم وسجلت نتائجهم في الجدول الآتي والمطلوب معرفة العلاقة بين أداء الطالب في اللعبتين.
| ضعيف | جيد جداً | مقبول | ممتاز | جيد | جيد جداً | ممتاز | جيد | ضعيف | جيد |
أداء الطالب في كرة اليد(X) |
| جيد | ضعيف | جيد | ممتاز | جيد جداً | جيد | جيد | مقبول | مقبول | ضعيف |
أداء الطالب في كرة القدم(Y) |
الحل:
نكون جدول نبين فيه رتب كل من Xi (كرة اليد) و Yi (كرة القدم) والفرق d ومربع الفرق d2 كالتالي:
|
رقم الطالب |
Xi |
Yi |
Rank X |
Rank Y |
d |
d2 |
|
1 |
جيد |
ضعيف |
6 |
9.5 |
– 3.5 |
12.25 |
|
2 |
ضعيف |
مقبول |
9.5 |
7.5 |
2 |
4 |
|
3 |
جيد |
مقبول |
6 |
7.5 |
– 1.5 |
2.25 |
|
4 |
ممتاز |
جيد |
1.5 |
4.5 |
– 3 |
9 |
|
5 |
جيد جداً | جيد |
3.5 |
4.5 |
– 1 |
1 |
|
6 |
جيد | جيد جداً |
6 |
2 |
4 |
16 |
|
7 |
ممتاز | ممتاز |
1.5 |
1 |
0.5 |
0.25 |
|
8 |
مقبول | جيد |
8 |
4.5 |
3.5 |
12.25 |
|
9 |
جيد جداً | ضعيف |
3.5 |
9.5 |
– 6 |
36 |
|
10 |
ضعيف | جيد |
9.5 |
4.5 |
5 |
25 |
|
Total |
0 |
118 |
||||
نعوض في القانون:
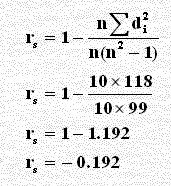
العلاقة بين الأداء في اللعبتين سالبة وضعيفة.
أو
نكون جدول نبين فيه رتب المستويات فالضعيف نعطيه رقم 1 و ... أي
|
ممتاز |
جيد جداً |
جيد |
مقبول |
ضعيف |
|
5 |
4 |
3 |
2 |
1 |
نكون جدول نبين فيه رتب كل من Xi (كرة اليد) و Yi (كرة القدم) والفرق d ومربع الفرق d2 كالتالي:
|
Xi |
Yi |
المستوى X |
المستوى Y |
Rank X |
Rank Y |
d |
d2 |
|
جيد |
ضعيف |
3 |
1 |
5 |
1.5 |
3.5 |
12.25 |
|
ضعيف |
مقبول |
1 |
2 |
1.5 |
3.5 |
– 2 |
4 |
|
جيد |
مقبول |
3 |
2 |
5 |
3.5 |
1.5 |
2.25 |
|
ممتاز |
جيد |
5 |
3 |
9.5 |
6.5 |
3 |
9 |
|
جيد جداً |
جيد |
4 |
3 |
7.5 |
6.5 |
1 |
1 |
|
جيد |
جيد جداً |
3 |
4 |
5 |
9 |
– 4 |
16 |
|
ممتاز |
ممتاز |
5 |
5 |
9.5 |
10 |
– 0.5 |
0.25 |
|
مقبول |
جيد |
2 |
3 |
3 |
6.5 |
– 3.5 |
12.25 |
|
جيد جداً |
ضعيف |
4 |
1 |
7.5 |
1.5 |
6 |
36 |
|
ضعيف |
جيد |
1 |
3 |
1.5 |
6.5 |
– 5 |
25 |
|
Total |
0 |
118 |
|||||
وهو نفس الجدول السابق وتكون نفس النتيجة السابقة rs = – 0.192 وعليه تكون العلاقة بين الأداء في اللعبتين سالبة وضعيفة.