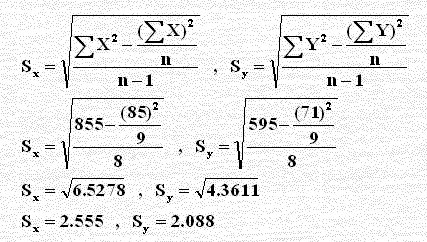
طريقة الدرجات المعيارية (Z)
إن متوسط ناتج ضرب كل درجتين معياريتين لقيم X, Y المتناظرة يمثل معامل ارتباط بيرسون حسب المعادلةr = (∑ZxZy) / (n–1)j وعليه نكون الجدول الآتي من خلال البيانات الأصلية:
|
X |
Y |
X2 | Y2 |
X – `X |
Y – `Y |
Zx = (X – `X) / Sx |
Zy = (Y – `Y) / Sy |
ZxZy |
| 6 | 4 | 36 | 16 | – 3.44 | – 3.89 | – 1.346 | – 1.863 | 2.508 |
| 8 | 8 | 64 | 64 | – 1.44 | 0.11 | – 0.564 | 0.053 | – 0.030 |
| 7 | 6 | 49 | 36 | – 2.44 | – 1.89 | – 0.955 | – 0.905 | 0.864 |
| 14 | 10 | 196 | 100 | 4.56 | 2.11 | 1.785 | 1.011 | 1.804 |
| 11 | 9 | 121 | 81 | 1.56 | 1.11 | 0.611 | 0.532 | 0.325 |
| 12 | 11 | 144 | 121 | 2.56 | 3.11 | 1.002 | 1.489 | 1.492 |
| 8 | 8 | 64 | 64 | – 1.44 | 0.11 | – 0.564 | 0.053 | – 0.030 |
| 9 | 7 | 81 | 49 | – 0.44 | – 0.89 | – 0.172 | – 0.426 | 0.073 |
| 10 | 8 | 100 | 64 | 0.56 | 0.11 | 0.219 | 0.053 | 0.012 |
| 85 / 9 = 9.44 | 71 / 9 =7.89 | 855 | 595 | 0.04 | 0 | 7.019 |
بتطبيق القانون الآتي لحساب قيمة الانحراف المعياري أولاً لكل منX, Y ومن ثم نحسب قيمة Z من Z = (X – `X ) / S نجد أنَّ:
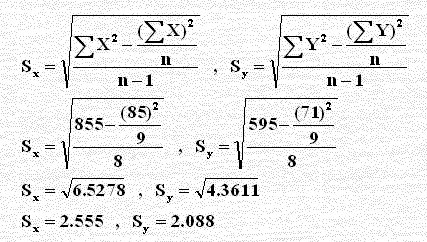
من الجدول العمود الأخير حاصل الجمع وبتطبيق القانونr = (∑ZxZy) / (n–1)j نجد أن:
r = 7.019/(9 - 1) = 7.019/8 = 7.019 / 8 = 0.877
وهو نفس قيمة معامل الارتباط في الحل السابق ونفس الاختبار السابق ذكره.