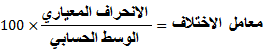
معامل الاختلاف(Coefficient of Variation):
يستخدم لمقارنة التشتت بين مجموعتين (المتغيرات النفسية) وذلك للاختلاف الواضح في الوسط الحسابي لمجموعتين من حيث القيمة فصغر الوسط الحسابي في المجموعة الأولى في مقابل كبره في المجموعة الثانية وهو النسبة المئوية بين الانحراف المعياري والوسط الحسابي وبالتالي لا يعتمد على وحدات المتغير الأصلي وبالتالي يمكن استخدامه لمجموعتين مختلفتين في الوحدات، ويحسب من الصيغة الرياضية الآتية:
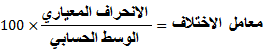
ويرمز له بالرمز Cv أو V أو CoV
الجدول التكراري الاتي يبين الدخل الشهري لـ 100 من المدرسين بالدينار:
|
المجموع |
-800 |
-700 |
-600 |
-500 |
-400 |
-300 |
الدخل |
|
100 |
5 |
12 |
20 |
35 |
12 |
16 |
العدد |
احسب معامل الاختلاف لهذا التوزيع وقارنه بتوزيع آخر وسطه الحسابي 550 دينار وانحرافه المعياري 80 دينار.
الحل: نكون الجدول التالي:
| المجموع | -800 | -700 | -600 | -500 | -400 | -300 | الدخل |
| 100 | 5 | 12 | 20 | 35 | 12 | 16 | التكرار(ك) |
| 850 | 750 | 650 | 550 | 450 | 350 | مركز الفئة | |
| 300 | 200 | 100 | 0 | -100 | -200 | الانحراف(ح) | |
| 3 | 2 | 1 | 0 | -1 | -2 | ح /100 | |
| 15 | 15 | 24 | 20 | 0 | -12 | -32 | ح × ك |
| 189 | 45 | 48 | 20 | 0 | 12 | 64 | ح2× ك |
الوسط الفرضي القيمة المقابلة لأكبر تكرار في مركز الفئة. باستخدام SPSS باستخدام Minitab
الوسط الحسابي = الوسط الفرضي + (مجـ( ح × ك) ÷ ن )× طول الفئة
Mean = 550 +(15÷ 100)×100 = 565
الانحراف المعياري σ

|
|
التوزيع الآخر:
Cv =i(80÷550)×100=14.6<24.3
التوزيع الآخر أقل تشتتاً