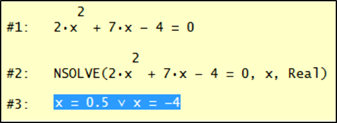|
المتغير |
↓الجذر الأول ↓ |
↓الجذر الآخر ↓ |
® |
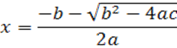
|

|
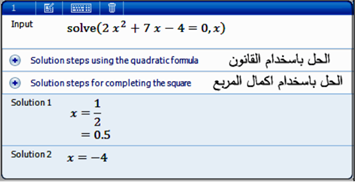
Microsoft Student |
الحل باستخدام برنامج |
|
|
|
х |
-4.00 |
0.500 |
المميز ¬ |
|
|
f(х) ®By
Cell B2 |
0.000 |
0.000 |
® |
|
Example:
f(х) = 2х2 + 7х - 4 = 0 |
|
نعوض في المميز في c2 ثم نستخدم Solver للجذر
الثاني |
|
f(х)=(2x─1)(x+4)=0 |
|
a = |
2 |
المعادلة تتغير بتغير المعاملات، x^2= x2 |
|
|
2х - 1 = 0 ® х1 = |
0.50 |
f(х)
اكتب معاملات الدالة → |
b = |
7 |
2x^2 + (7)x + (-4) = 0 |
|
|
х + 4 = 0 ® х2 = |
-4.00 |
|
c = |
-4 |
9 |
المميز = |
0.500 |
-4.000 |
|
|
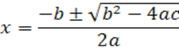
|
|
|
|
|
|
|
+ |
─ |
|
|
|
حُسبَ جذرا
المعادلة من |
х1 = |
-4 |
الحل
باستخدام المميز ¾¬ |
|
|
اضغط على علامة
"+" أعلاه للحل كاملاً (في البرنامج). |
|
|
القوانين
أعلاه أو من ¾¬ |
х2 = |
0.5 |
|
|
الحل استخدام Derive |
|
|
الحل باستخدام Mathematical |
بصرف النظر عن تسميتهما |
هما جذرا المعادلة |
х1 , х2 = |
0.5, -4 |
|
|
|
|
Solve[2x2+7x-4= =0,x] |
2x + (-1) = 0 |
2 |
-1 |
¾® |
x1 = |
0.5 |
↑لمعادلة الدرجة الثانية |
|
|
{{x ® -4}, {x
® 1/2}} |
الحل
باستخدام القسمة المطولة للجذر x2 |
|
|
2 |
7 |
-4 |
2x2 + 7x - 4 = 0 |
|
|
|
1 |
4.000 |
2 |
8 |
|
|
|
|
|
الحل استخدام Matlab 11 |
x + 4 = 0 |
0 |
-1 |
-4 |
|
|
|
|
>> roots([2,7,-4]) |
x2 = |
-4 |
|
-1 |
-4 |
|
|
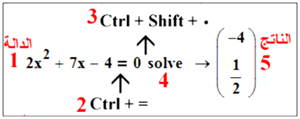
الحل باستخدام Maple 18 |
|
|
ans = |
|
|
|
0 |
0 |
|
|
{-4, 1/2} ¬¾ |
{solve(2x2+7x-4 = 0, x)} |
|
|
-4 |
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|