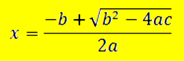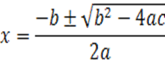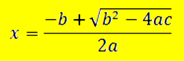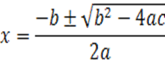| المتغير |
↓الجذر الأول ↓ |
↓الجذر الآخر ↓ |
® |
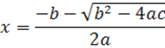
|
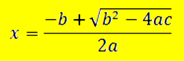
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| х |
0.50 |
-4.00 |
|
|
|
|
|
| f(х) ® Cell B3 |
0.000 |
0.000 |
® |
|
|
| Example:
f(х)= |
2х2 + 7х - 4 = 0 |
|
نعوض في المميز في c1 ثم نستخدم Solver للجذر
الثاني |
|
| f(х)=(2x─1)(x+4)=0 |
|
a = |
2 |
المعادلة تتغير بتغير المعاملات، x^2= x2 |
|
|
| х1 |
0.50 |
f(х)
معاملات الدالة → |
b = |
7 |
2x^2 + (7)x + (-4) = 0 |
|
|
| х2 |
-4.00 |
|
c = |
-4 |
9 |
المميز = |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
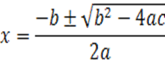
|
حُسبَ جذرا
المعادلة من |
х1 = |
-4 |
الحل
باستخدام المميز ¾¬ |
|
|
x |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
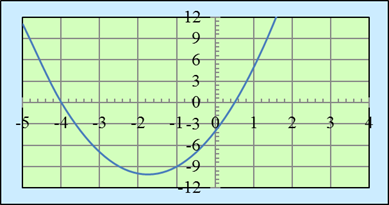
| القوانين أعلاه أو من القانون ¾¬ |
х2 = |
0.5 |
|
|
f(x) |
11 |
0 |
-7 |
-10 |
-9 |
-4 |
5 |
18 |
35 |
56 |
|
|
|
|
|
|
|
f(х) = 2х2 + 7х ─ 4
= 0 |
Example4, 8 ® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|