
الالتواء SKEWNESS
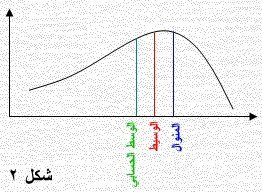
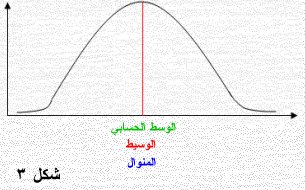
التوزيع التكراري المتماثل ما كانت تكراراته موزعة توزيعاً متماثلاً حول وسطه الحسابي بما يعني قيم المتغير المتساوية البعد عن الوسط الحسابي لها نفس التكرار فالتواء توزيع يعني مدى بعده عن التماثل وقد يكون الالتواء جهة اليمين (موجب الالتواء) أو الالتواء جهة اليسار (سالب الالتواء) والأشكال الثلاثة التالية تبين ذلك:



فالشكل 1 التواء جهة اليمين ، الشكل 2 التواء جهة اليسار ، الشكل 3 متماثل، وبافتراض أن هذه الأشكال تمثل درجات طلاب في امتحان ما، ففي الشكل 1 يعني عدد كبير من الطلاب حصلوا على درجات أقل من المتوسط بمعنى أن مستوى الطلاب أقل من مستوى الامتحان أو أن الامتحان صعب في حين العكس تماماً في الشكل 2 حيث يبن أن عدد كبير من الطلاب حصلوا على درجات أكبر من المتوسط أي أن مستوى الطلاب أعلى من مستوى الامتحان أو أن الامتحان سهل في حين الشكل 3 يعنى مستوى الطلاب مناسب لمستوى الامتحان.
يقاس الالتواء بأحد المقياسين الآتيين:
3 (`X – MD )
SKEWNESS = ——————— , MD الوسيط , S الانحراف المعياري
S
∑ ( Xi –`X )3
SKEWNESS = ——————— , i = 1, 2, ..., N
S3 ( N – 1 )
وهي مقاييس نسبية يمكن استخدامها للمقارنة بين التواء التوزيعات كما أن قيمة مقياس الالتواء محصورة بين i+3 ، – 3فالقيمة السالبة تعني الالتواء جهة اليسار والقيمة الموجبة تعني الالتواء جهة اليمين والقيمة صفر تعني عدم وجود التواء أو التماثل (التوزيع متماثل).
التفرطح (KURTOSIS or PEAKEDNESS)
التفرطح ثلاثة أنواع للمنحنيات التكرارية (مقارنة بالمنحنيات المعتدلة):
1) متوسط التفرطح (معتدل) ( Mesokurtic ( Norma
2) مدبب ( Leptokurtic ) معظم القيم بالقرب من الوسط الحسابي والذيلين
3) مفرطح ( Platykurtic ) معظم القيم بعيدة عن الوسط والذيلين
يحسب من الصيغة الرياضية:
∑ ( Xi –`X )4
KURTOSIS = ——————— , i = 1, 2, ..., N
S4 ( N – 1 )