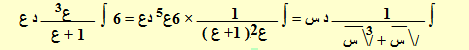
إذا أشتملت الدالة على أس كسري للمتغير س فقط فيلزم التعويض س = عن حيث ن المضاعف المشترك لمقامات الأسس الكسرية للمتغير س فتؤول الدالة لكسر جبري قياسي.
مثال:
1
احسب ∫ ـــــــــــــــــــــــــــــــ د س
ـــــ 3 ــــــ
/\ س + /\ س
الحل:
الفكرة:
من الواضح هنا أن مقام أسس س هي 2 ، 3 والمضاعف المشترك هو 6 أي نضع س = ع6 فيكون دس = 6ع5 دع وإذا عوضنا عن س في المقام لحصلنا على ع3 + ع2 أي ع2(ع + 1) والبسط يكون هو دس أي 6ع5 دع فنحصل على ع3 في البسط و ع+1 في المقام ويلزم هنا القسمة المطولة ويسهل التكامل بعد ذلك.
ع2 – ع + 1
ـــــــــــــــــــــــــــــــــــــــــــــ
ع3 │ ع + 1
ــــــــــــــــ
ع3 + ع2
ـــــــــــــــــــــــــــــــــــــــ
0 – ع2
ــــــــــــــــــــــــــــــــــــــ
– ع2 – ع
ـــــــــــــــــــــــــــــــــــــ
0 + ع
ـــــــــــــــــــــــــــــــــــــ
ع + 1
ـــــــــــــــــــــــــــــــــــــ
0 – 1 (الباقي –1)
ـــــــ 3 ــــــــ 3 ــــــــ 6 ـــــــ
المقام = /\ س + /\ س = /\ س ( 1 + /\ س ) ....... (1)
الأسس الكسرية هنا مقامها 3 ، 6 والمضاعف المشترك لها هو 6 وعليه يكون:
بوضع س = ع6 فيكون بالاشتقاق: د س = 6 ع5 د ع والتعويض في ... (1)
المقام = ع2(1 + ع)
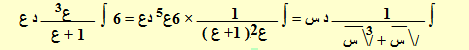
بالقسمة المطولة ع3 على 1 + ع نجد أن الناتج ع2 – ع + 1 والباقي –1 ( سبق إجراء القسمة أعلاه)
ع3 1
∫ ــــــــــــــ د ع = 6∫ (ع2 – ع + 1 – ــــــــــــــ ) د ع
1+ ع 1 + ع
ع3 ع2
=6(ـــــــ – ـــــ + ع – لـو (1 + ع) + ث
3 2
= 2ع3 – 3ع2 + 6ع –6 لـو(1+ ع) + ث وبالتعويض من س = ع6 نجد أن:
ــــ 3 ــــ 6 ـــــ 6 ـــــ
= 2/\س – 3/\س + 6/\س –6 لـو(1 + /\س ) + ث
ملاحظة:
في حال وجود (أ + ب س) كأساس لأس غير صحيح نضع (أ + ب س) = عن