∫ حامس حتانس د س
الحالة الثالثة : مجموع م ، ن عدد زوجي سالب
ــــــــــــــــ
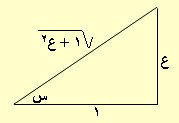
بوضع طاس = ع فبرسم
مثلث قائم للزاوية س ظلها = ع : 1 فيكون الوتر /\ 1 +
ع2 ,
ــــــــــــــــ
حاس = ع : /\ 1 + ع2
ــــــــــــــــ
حتاس = 1: /\ 1 + ع2
وبالاشتقاق طاس = ع يكون قا2س د س = د ع
وبالتعويض عن حاس ، حتاس ، د س بدلالة ع
نحصل على صورة يسهل تكاملها ثم نعوض عن ع كما هو مبين بالمثال التالي.
1
مثال : أحسب ∫ ـــــــــــــــــــــــــــ د س
حا2س حتا4س
ــــــــــــــــ ــــــــــــــــ ــــــــــــــــ
بوضع طاس = ع فبرسم مثلث قائم للزاوية س ظلها = ع : 1 فيكون الوتر /\ 1 + ع2 ، حاس = ع : /\ 1 + ع2 ، حتاس =1: /\ 1 + ع2
وبالاشتقاق يكون قا2س د س = د ع ومنها د س = د ع ÷ قا2س مع ملاحظة قا2س = 1 + طا2س أي د س = د ع ÷ (1 + ع2) ،
ع2 1
حا2س = ــــــــــــــــــــــــ ، حتا4س = ــــــــــــــــــــــــ بالتعويض مع ملاحظة حا2س ، حتا4س في المقام فتقلب نتائجها فيكون
1 + ع2 (1 + ع2)2
1 ( 1 + ع2 ) ( 1 + ع2 )2 1
∫ ـــــــــــــــــــــــــــ د س = ∫ ــــــــــــــــــــــ × ـــــــــــــــــــــــــ × ــــــــــــــــــــــــ د ع بالاختصار وفك القوس
حا2س حتا4س ع2 1 ( 1 + ع2 )
1 + 2ع2 + ع4
= ∫ ــــــــــــــــــــــــــــــــ د ع
ع2
= ∫ ( ع–2 + 2 + ع2 ) د ع
1 ع3
= – ــــــ + 2 ع + ــــــ + ث ، ع = طاس ومقلوب طاس هو طتاس وبالتعويض عن ع = طاس
ع 3
1
= – طتاس + 2 طاس + ــــ طا3س + ث
3