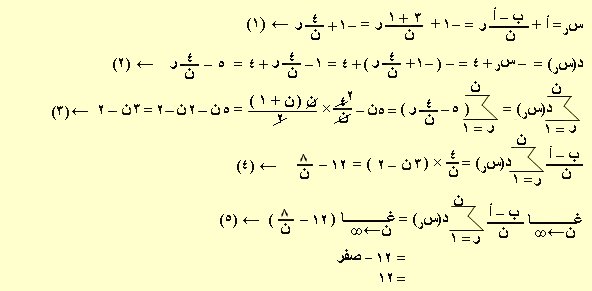
+ + + + + 0 – – – – –

الفترة [ –1، 3 ] = [ أ ، ب ]    ، د(س) = | س – 4|                 ـــــــــــــــــــــــــــــــــــــــــــــ ح    س = 4 تجعل قيمة المقياس صفر

                                                                                                    4  

دالة المقياس يجب إعادة تعريف المقياس وهو في حالات ثلاث بكون د(س) قبل الفترة أو بعدها أو تجمعهم وسنوضح ذلك كالآتي :

في مثالنا هذا قيمة س التي تجعل المقياس يساوي صفراً هي س = 4 وهي  على يمين الفترة [ –1، 3 ] أي الدالة سالبة –(س –4)

أي د(س) = – (س –4) = – س + 4 وإن كانت على يسار الفترة كانت الدالة موجبة وإن كانت تنتمي للفترة فيكون التكامل في فترتين.

                                        ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ

                                                                4        3        2        1        0        –1

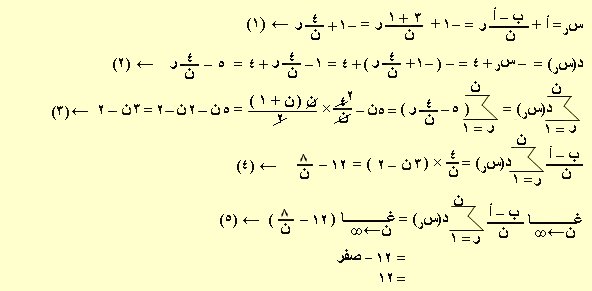
باستخدام المساحة

نوجد قيم د(3) ، د(–1)

د(3) = –(3 – 4 ) = 1 والنقطة ( 3 ، 1 )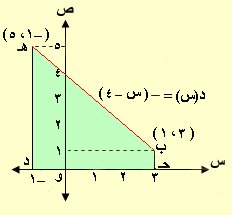

د(–1) = –( –1 – 4 ) = 5 والنقطة ( –1 ، 5 )

نرسم منحنى الدالة الذي يمثله ب هـ ( خط مستقيم)

من المعلوم المساحة فوق محور السينات موجبة

والمساحة تحت منحنى د(س) = – (س – 4) ومحور السينات والمستقيمان س= –1، س= 3

هي مساحة شبه المنحرف ب حـ د هـ

                           1 + 5 

المساحة المطلوبة = ـــــــــــــ × 4 = 6 × 2 = 12

                               2

  3

 ∫  | س – 4 | د س = 12     وهي نفس النتيجة باستخدام التجزيء النوني المنتظم

–1