dx
Find: ∫ ———————
( 3cosx + 4sinx)
2 dz
z = tan (x/2), x/2 = tan–1(z), x = 2 tan–1(z), dx = ———
1+ z2
x 2 2 2 2 – 1 – z2 1 – z2
cos x = 2 cos2 (—) – 1 = ————— – 1 = —————— – 1 = ———— – 1 = ————— = ———
2 sec2(x/2) 1 + tan2(x/2) 1 + z2 1 + z2 1 + z2
sin(x/2) tan(x/2) tan(x/2) 2 z
sin x = 2 sin(x/2) cos(x/2) = 2 ———— . cos2(x/2) = ———— = —————— = ———
cos(x/2) sec2(x/2) 1 + tan2(x/2) 1 + z2
1 – z2 2 z 3 – 3 z2 + 8 z
3cosx + 4sinx = 3 —–—— + 4 ——— = ——————
1 + z2 1 + z2 1 + z2
dx 2 dz 1 + z2
∫
——————— = ∫
——— .—————— 
( 3cosx + 4sinx) 1+ z2 3 – 3 z2 + 8 z
– 2 dz
= ∫ ——————
3 z2 – 8 z – 3
– 2 dz
= ∫ ——————
(3z + 1)(z – 3)
3 dz 1 dz
=∫ [ — . ——— – — . ——— ]
5 3z + 1 5 z – 3
1 3dz dz
= —[ ∫ ——— – ∫ ——— ]
5 3z + 1 z – 3
1
= — [ Ln ( 3z + 1) – Ln ( z – 3) ] + c .......... (1)
5
(Note Ln(a), must a>0)
1 x x
=— [ Ln ( 3 tan — + 1) – Ln (3 – tan — ) ] + c
5 2 2
OR. Continue ...... (1)
sin(x/2) sin(x/2) 2 cos(x/2) 2 sin(x/2) cos(x/2) sinx
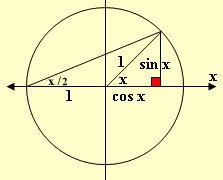
z = tan(x/2) = ——— = ———— . ———— = ———————— = ———— OR see draw
cos(x/2) cos(x/2) 2 cos(x/2) 2 cos2(x/2) 1 + cosx
1 sin x
= — [ Ln ( 3z + 1) – Ln ( z – 3) ] + c ( but z = tan(x/2) = ———— ( see draw )
5 1 + cosx
1 3 sin x sin x
= — [ Ln ( ———— + 1) – Ln ( 3 – ———— ) ] + c (Note Ln(a), must a>0)
5 1 + cosx 1 + cosx
1 1 + cosx + 3sinx 3cosx – sinx + 3
= — [ Ln ( ———————— ) – Ln ( ——————— ) ] + c (Ln a/b = Ln a – Ln b)
5 1 + cosx 1 + cosx
1
= — [ Ln ( 3 sin x + cosx + 1) – Ln ( 3cosx – sinx + 3 ) ] + c
5