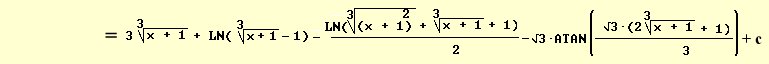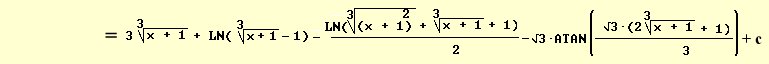
3 ———
\/ x + 1
Example4: Find ∫———— dx
x
let:
3 ———
z = \/ x + 1 Then z3 = x + 1 , x = z3 – 1 , dx = 3z2 dz
3 ———
\/ x + 1 z 3z3 dz
∫ ———— dx = ∫——— . 3z2 dz = ∫ ———
x z3 – 1 z3 – 1
نستخدم القسمة المطولة
3
———
3z3 | z3 – 1
————
3z3 – 3
————
0 + 3
3 ———
\/ x + 1 3dz
∫ ———— dx =3 ∫ dz + ∫ —————————
x ( z – 1)( z2 + z + 1 )
باستخدام الكسور الجزئية
3 ———
\/ x + 1 1 z + 2
∫ ———— dx =3 ∫ dz + ∫[ ——— – ————— ] dz
x z – 1 z2 + z + 1
1 1 2 z + 4
=3 ∫ dz + ∫[ ——— – — . ———— ] dz
z – 1 2 z2 + z + 1
1 1 2 z + 1 + 3
=3 ∫ dz + ∫[ ——— – — . ————— ] dz
z – 1 2 z2 + z + 1
1 1 2 z + 1 1 3
=3 ∫ dz + ∫[ ——— – — . ————— + — . ————— ] dz
z – 1 2 z2 + z + 1 2 z2 + z + 1
1 1 x
Last integration: z2 + z + 1= ( x + 1/2)2 + 3/4 , We have: ∫ ———— dz = — ATAN( ——) + c
z2 + a2 a a
Ln(z2 + z + 1) — 2z + 1
=3 z + Ln(z – 1) – ——————— – \/ 3 ATAN ———— + c " Atanx = tan–1x "
—
2 \/ 3
بالتعويض