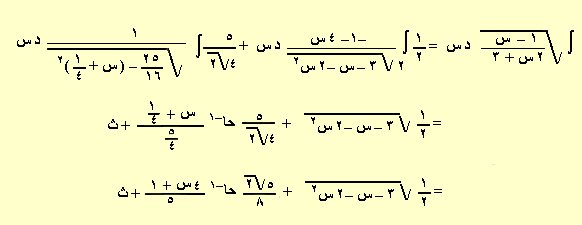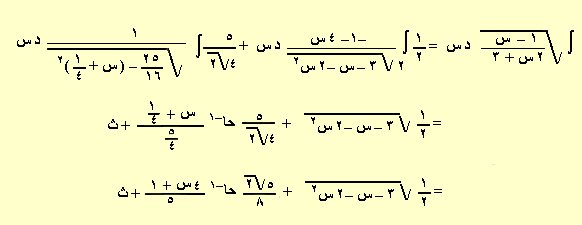
ــــــــــــــــــــــــ
ب س + حـ
ـــــــــــــــــــــ
/\ ل + ك س
ـــــــــــــــــــــــ
بالضرب في /\ ب س + حـ فيصبح البسط ب س + حـ في حين المقام وبعد ضرب القوسين (ل + ك س)(ب س + حـ) نحصل على الصورة:
د س2 + هـ س + و أي تتحول المسألة للصورة الآتية السابق شرحها وهي:
ل + ك س
ــــــــــــــــــــــــــــــــــــــــــ حيث نجعل البسط مشتقة ما تحت الجذر في المقام ومن ثم نجزئ الكسر كما سبق ذكره
ـــــــــــــــــــــــــــــــــــ
/\ أس2 + ب س + حـ
ــــــــــــــــــــــ
1 – س
مثال : أوجد ∫ ـــــــــــــــــــــ د س
/\2 س + 3
ـــــــــــــ
بالضرب في /\1– س فنحصل على كسر بسطه 1– س ومقامه (1– س)(2 س + 3) = 3 – س –2 س2 مشتقته –1– 4 س
ــــــــــــــــــــــ
1 – س 1 – س
∫ ـــــــــــــــــــــ د س = ∫ ــــــــــــــــــــــــــــــــــــ د س
/\2 س + 3 ــــــــــــــــــــــــــــــــ
/\ 3 – س –2 س2
لنجعل البسط مشتقة (3 – س –2 س2 ) أي 1– س ليصبح –1– 4 س حيث سنضرب في ونقسم على 4 ثم نكمل كما يلي:
1 1 1 5
1– س = ــــ ( 4 – 4 س ) = ـــ ( –1–4 س + 5) = ـــ ( –1– 4 س) + ـــ وعليه يكون :
4 4 4 4
ــــــــــــــــــــــ
1 – س 1 –1– 4 س 5 1
∫ ـــــــــــــــــــــ د س = ـــ ∫ ــــــــــــــــــــــــــــــــــــ د س + ــــ ∫ ــــــــــــــــــــــــــــــــــــ د س
/\2 س + 3 4 ــــــــــــــــــــــــــــــــ 4 ــــــــــــــــــــــــــــــــ
/\ 3 – س –2 س2 /\ 3 – س –2 س2
سنجزئ 4 إلى 2 × 2 بالنسبة للتكامل الأول في الطرف الأيسر ليكون ناتج التكامل هو المقام أي:
3 1 3 1 1 1 25 1
سنجعل 3 – س –2 س2= 2( ــــ – ــــ س – س2) = 2[ ــــ + ـــــ – ( س2+ ــــ س + ـــــ )] = 2[ ـــــــ – ( س + ــــ )2]
2 2 2 16 2 16 16 4
وبإخراج 2 خارج الجذر نحصل على التكامل حسب القاعدة فيكون :