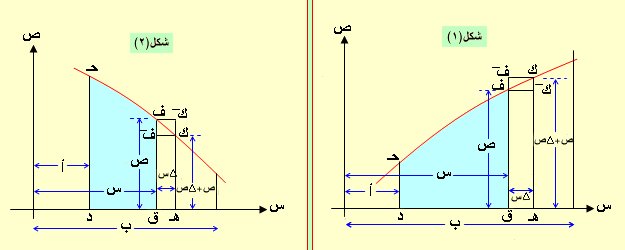
المعنى الهندسي للتكامل :

إن التكامل المحدود لدالة من س = أ إلى س = ب يمثل هندسياً بالمساحة المحدودة بمنحنى الدالة ومحور السينات والمستقيمين س = أ ، س = ب

لتكن م مساحة المنطقة حـ ف ق د والمحدودة بمنحنى ومحور السينات ، حـ د ، ف ق والناشئة من حركة حـ د إلى ف ق فالمساحة متغيرة أي دالة للمتغير س ولنحدث تغير قدره ∆ س (ق هـ) فتكون ك هي المناظرة على المنحنى ويكون هـ ك = ص + ∆ ص ومساحة ف ق هـ ك(∆ م) مقدار التغير في مساحة حـ ف ق د نتيجة التغير في س قدره ∆ س.

فمن شكل(1) : مساحة ف¯ق هـ ك > ∆ م > مساحة ف ق هـ ك¯     .... (1)     ميل المنحنى ف ك موجب

ومن شكل(2): مساحة ف ق هـ ك¯ > ∆ م > مساحة ف¯ ق هـ ك    .... (2)     ميل المنحنى ف ك سالب

من (1) : ( ص + ∆ ص ) . ∆ س > ∆ م > ص . ∆ س     بالقسمة على ∆ س

                                       ∆ م

             ( ص + ∆ ص ) > ــــــــــ > ص    عندما ∆ س تقترب من الصفر فإنَّ ∆ ص تقترب من الصفر أيضاً فيكون :

                                      ∆ س

                  د م

               ــــــــــ = ص    وباعتبار ص = د^/ (س) معادلة المنحنى حيث د^/ (س) المشتقة الأولى للدالة د(س) فإن :

                 د س

            م = ∫ ص د س  أي أن :

            م = ∫ د^/ (س) د س = د(س) + ث ولكن المساحة = 0 عندما س = أ  أي 0 = د(أ) + ث أي ث = – د(أ) فتكون :

            م = د(س) – د(أ) ولحساب المساحة من س = أ إلى س = ب نضع س = ب فإن :

                                    ب

            م = د(ب) – د(أ) = ∫ د^/ (س) د س وعليه يكون

                                     أ

                ب

                ∫ د^/ (س) د س = د(ب) – د(أ)  وعليه يكون:

                أ

             ب

             ∫ د^/ (س) د س = مساحة المنطقة المحدودة بمنحى د^/ (س) ومحور السينات والمستقيمين س = أ ، س = ب

             أ

فالتكامل المحدود لأي دالة من س = أ إلى س = ب يمثل هندسياً بالمساحة المحدودة بمنحنى الدالة ومحور السينات والمستقيمين س= أ ، س= ب

من(2) : ص . ∆ س > ∆ م > ( ص + ∆ ص ) . ∆ س    بالقسمة على ∆ س

                        ∆ م

              ص > ــــــــــ >( ص+ ∆ ص )   

                       ∆ س

    ونكمل كما سبق لنحصل على نفس النتيجة