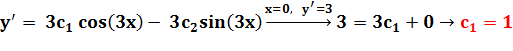المعادلة التفاضلية (Differential equation) هي معادلة تحوي تفاضلات وتظهر فيها بشكل متغيرات المعادلة.
ويكون الهدف من حل المعادلة
هو إيجاد الدالة الرياضية التي تحقق مشتقات هذه المعادلة.
وتبرز المعادلات التفاضلية
بشكل كبير في تطبيقات الفيزياء والكيمياء، وحتى النماذج الرياضية
المتعلقة بالعمليات الحيوية والاجتماعية والاقتصادية.
تعرف رتبة المعادلة
التفاضلية على أنها أعلى رتبة لمشتق موجود في هذه المعادلة.
y'' + 2 y' – 3 = 4 x معادلة تفاضلية من الرتبة الثانية
y'''' + 2 y'' – 3y = 4 x معادلة
تفاضلية من الرتبة الرابعة
تعرف درجة المعادلة بالأس
التي رفع إليه أعلى تفاضل في المعادلة التفاضلية.
(y'')3 + 2
(y')6 – 3 = 4 x معادلة تفاضلية من الدرجة الثالثة
(y'''')4 + 2
y'' – 3y = 0 معادلة تفاضلية من الدرجة
الرابعة
حل
المعادلة التفاضلية y''(x) + 9 y = 0 دالة تحققها أي y = c1
sin(3x) + c2 cos(3x)
نقول
ان y = c1 sin(3x) + c2 cos(3x) حل للمعادلة التفاضلية y''(x)
+ 9 y = 0
الحل العام للمعادلة التفاضلية
ما كان عدد الثوابت في الحل يساوي رتبتها مثال:
y = c1 sin(2x) + c2 cos(2x) حل عام لأن عدد الثوابت 2 ورتبة المعادلة 2
الحل الخاص للمعادلة التفاضلية
هو حلها العام بعد معرفة قيم الثوابت:
فإذا كان y(0) = 2 , y'(0) = 3 فإنَّ 1= c1 وإن 2 = c2 أي: y = sin(3x) + 2 cos(3x) هو الحل الخاص حيث أنَّ:
![]()