تمرين محلول:
أ ب حـ مثلث رسم على أضلاعه مثلثات متساوية الأضلاع خارج المثلث أ ب و ،
ب حـ د ، جـ أ هـ أثبت أن :
1ـ أ د = ب
هـ = حـ و
2ـ أ
د، ب هـ ، جـ و تتلاقى في نقطة واحدة ولتكن ن
3ـ كل أثنين من المستقيمات الستة المتفرعة من ن يحصران بينهما زاوية 60
درجة
4ـ الدوائر
أ ب و ، ب حـ د ،
حـ أ هـ تمر كلها بنقطة ن
5ـ ن د = ن
ب + ن حـ ، ن
و = ن أ + ن ب ، ن
هـ = ن أ + أ حـ
6ـ في
الشكل
الرباعي
غير الدائري المستطيل المكون من القطرين اصغر من مجموع المستطيلين المكون كل منهما من ضلعين متقابلين في الشكل المذكور
7ـ أوجد نقطة ن داخل المثلث بحيث ن أ + ن ب + ن حـ نهاية صغرى
الحـــــــل
1)
المثلثان أ ب د ، و ب جـ متطابقان وينتج أن أ د = و حـ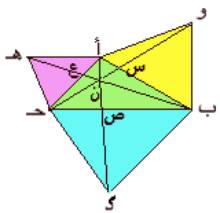
والمثلثان أ حـ و ، أ هـ ب متطابقان وينتج أن حـ و = هـ ب
ومما سبق ينتج أن أ د = ب هـ = حـ و
2) أ س
:
س ب
=
مساحة أ س و
: مساحة ب س و=
مساحة أ س حـ
: مساحة ب
س حـ
= (مساحة أ س و+
مساحة أ س حـ):(مساحة ب س و+ مساحة ب س حـ(
= مساحة أ و حـ : مساحة ب حـ و --------------
(1)
بالمثل ب ص : ص حـ = مساحة أ ب د : مساحة
أ حـ د --------
(2)
بالمثل حـ ع : ع أ = مساحة ب حـ هـ : أ ب هـ --------------
(3)
من (1) ، (2) ، (3)
مساحة أ ب د = مساحة و ب حـ ،
مساحة أ حـ د = مساحة هـ حـ ب ،
مساحة أ و حـ = مساحة أ ب هـ
أ س : س ب × ب ص : ص حـ × حـ ع : ع أ = 1 فإن أد ، ب هـ ، حـ و تتلاقى في نقطة واحدة (نظرية)
3) من تطابق المثلثين
أ ب د ، و ب حـ ينتج أن < أ د ب = < و حـ ب وهما على ب ن وفي جهة واحدة منه
إذن الشكل ن ب حـ د
رباعي دائري
وبالمثل يمكن إثبات أن
: أ ن ب و ، أ ن حـ هـ رباعي دائري
إذن < ب ن د = <
ب حـ د = 60 ، < حـ ن و = < حـ ب د = 60 ،
< أ ن و = < أ ب و = 60 ، < ب ن و = < ب أ و = 60
،
< أ ن هـ = < أ حـ هـ = 60 ، < حـ ن هـ = < حـ أ هـ = 60
4) أ و ب ن رباعي
دائري فالدائرة المارة به تمر بالنقطة ن وهي مارة بالمثلث أ ب و ومثله للشكلين ب د
حـ ن ، أ هـ حـ ن
إذن الدوائر المارة بـ أ ب و ، ب حـ د ، أ حـ هـ تمر بـ ن فهي تتقاطع في
النقطة ن
5) بما أن ب ن حـ د رباعي دائري
إذن ن د . ب حـ = ن ب . حـ د
+ ن حـ . ب د نظرية بطليموس
ن د = ن ب + ن حـ حيث المثلث ب حـ د متساوي الأضلاع
بالمثل يكون : ن و = ن أ + ن ب ، ن هـ = ن أ + ن حـ
6) هنا يوجد عمل وهو
رسم د هـ بحيث يكون < ب حـ أ = < أ د هـ ، ورسم أ هـ بحيث يكون < ب أ هـ
= < حـ أ د ، نصل ب هـ
< ب أ
حـ = < هـ أ د( بإضافة < هـ أ حـ لكل من الزاويتين ب أ هـ ، حـ أ د(
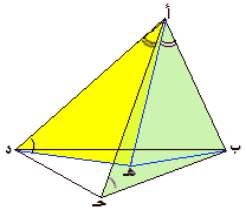
وحيث أن < ب حـ أ = <
أ د هـ فالمثلثان أب حـ ، أ هـ د متشابهان
إذن أ ب : أ هـ = أ حـ : أ د = ب حـ :
هـ د ---- (1)
المثلثان أ ب هـ ، أ حـ د
فيهما < ب أ هـ = < حـ أ د عملاً ،
ب أ : أ حـ = أ هـ : أ د من (1)
إذن المثلثان متشابهان وينتج
ب أ : أ حـ = أ هـ : أ د = ب هـ : حـ د
--- (2)
من (1) ينتج أن ب حـ . أ د = أ حـ . هـ د
من (2) ينتج أن أ ب . حـ د = أ حـ . ب هـ
بالجمع ينتج أن أ ب . حـ د + ب حـ . أ د = أ حـ( ب
هـ + هـ د )
وحيث أن (ب هـ + هـ د) > ب د مجموع ضلعين في مثلث أكبر من الثالث
إذن أن أ ب . حـ د + ب حـ . أ > أ حـ . ب د
7) العمل
نرسم ( خارج المثلث أ ب حـ) المثلث ب حـ د المتساوي الأضلاع ونصل أ د
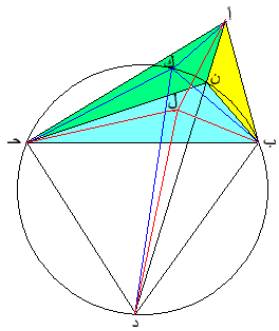
ليقطع محيط الدائرة في ن
فتكون النقطة المطلوبة
نعلم أن أ د = ن أ + ن ب + ن
حـ
( ن ب د حـ رباعي دائي ونظرية بطليموس والاختصار)
بفرض ل نقطة داخل المثلث أ ب
حـ فأن ل أما تقع على محيط الدائرة
أو لا تقع فإن وقعت ولتكن ك كان ك د = ك ب + ك حـ
( لا حظ الشكل
الراعي الدائري وبطليموس أفندي)
ك أ + ك ب + ك حـ = ك أ + ك د > أ د
أي أكبر من ن أ + ن ب + ن حـ أي
ن أ + ن ب + ن حـ < ك أ +
ك ب + ك حـ
فإن لم تقع مثل ل فإن الشكل
ب ل حـ د رباعي غير دائري
إذن ب ل . حـ د + حـ ل . ب د
> د ل . ب حـ ( تمرين 6 )
بما أن حـ د = ب د = ب
حـ فيمكن اختصر المتباينة أعلاه
إذن ب ل + حـ ل > د
ل
إذن ب ل + حـ ل + أ ل
> د ل + أ ل ( بإضافة أ ل )
أي ب ل + حـ ل + أ ل > أ د (لأن د ل + أ
ل > أ د)
أي أكبر من ن أ + ن ب
+ ن حـ
أي أن ن أ + ن ب + ن حـ < ل أ + ل ب + ل
حـ
وبالمثل يمكن
إثبات أن ن أ + ن ب + ن حـ أصفر من مجموع أبعاد أي نقطة أخرى
داخل المثلث أ ب حـ ، أي أن ن هي النقطة المطلوبة *** قد يكون هناك حل آخر***