مثال:

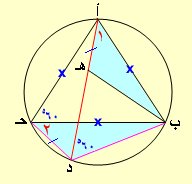
أ ب حـ مثلث متساوي الأضلاع مرسوم داخل دائرة، أخذت النقطة د على القوس الأصغر ب حـ والمطلوب إثبات أن:

أ د = حـ د + ب د

مقدمة:

1) المثلث المتساوي الأضلاع كل من زواياه الثلاثة يساوي 60^ه

2) في الشكل الرباعي الدائري تكون الزوايا المحيطية والمرسومة على قوس واحد متساوية

3) الزاوية الخارجة عن الشكل الرباعي(بامتداد أحد أضلاعه) = الزاوية المقابلة للمجاورة لها

4) يتطابق المثلثان في عدة حالات (يراجع)

العمل:

    نأخذ القطة هـ على أ د بحيث أ هـ = حـ د

البرهان:

    من الشكل نجد أن: <1 = < 2 محيطية ، < ب د أ = < أ حـ ب =  60^ه محيطية

    المثلثان أ ب هـ ، حـ ب د فيهما:

        أ هـ = حـ د     عملاً

        أ ب = ب حـ                       من مثلث متساوي الأضلاع

        ق< 1 =  ق< 2                 مرسومة على القوس ب د (محيطية)

    \ يتطابق المثلثان وينتج أن:

        ب هـ = ب د

    ¼ ق< ب د أ = 60^ه                  ¼  تعني بما أنَّ

    \ ق< ب هـ د  = 60^ه 

    \ ق<هـ ب د  = 60^ه                      مجموع زوايا المثلث = 180^ه

    \ المثلث ب هـ د متساوي الأضلاع     لتساوي زواياه الثلاث

    \ ب د = هـ د

    \ ب د + حـ د = هـ د + هـ أ

    \ ب د + حـ د = أ د        وهو المطلوب

حـل آخـر :  

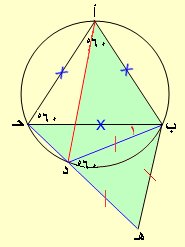
العمــــل:

    نمد حـ د إلى هـ بحيث د هـ = د ب    

البرهان:

    ق< ب د هـ = ق< ب أ حـ = 60^ه         خارجة عن الشكل الرباعي

    ¼ د ب = هـ ب

    \ ق< د ب هـ = ق<  د هـ ب = 60^ه  مجموع زوايا المثلث 180^ه

    \ ب د = ب هـ          لاحظ المثلث د ب هـ متساوي الأضلاع

    المثلثان أ ب د ، حـ ب هـ فيهما:

        أ ب = ب حـ         المثلث أ ب حـ متساوي الأضلاع

        ب د = ب هـ         إثباتاً

        ق< أ ب د = ق< حـ ب هـ     بإضافة <1 لكل من < أ ب حـ ، د ب هـ المتساويتان (60^ه)

    \ يتطابق المثلثان وينتج أن:

        أ د = حـ هـ    

        أ د = حـ د + د هـ

        أ د = حـ د + د ب            وهو المطلوب

حل ثالث: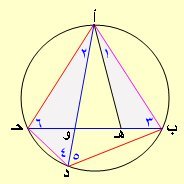

    توجد نظرية تنص:

        في الشكل الرباعي الدائري المستطيل المكون من قطريه يكافئ مجموع المستطيلين المكونين من

        كل ضلعين متقابلين فيه.

البرهان:

    بفرض طول ضلع المثلث أ ب حـ المتساوي الأضلاع يساوي ل

   ¼ الشكل أ ب د حـ رباعي دائري

   \ أ د × ب حـ = أ ب × د حـ + أ حـ × ب د

   \ أ د × ل = ل × د حـ + ل × ب د         بالقسمة على ل ≠ صفر

   \ ا د = د حـ + ب د                            وهو المطلوب

برهان النظرية:

في الشكل :

    أخذت النقطة هـ على ب حـ بحث ق< ب أ هـ = ق< د أ حـ ( أي < 1 = < 2

    المثلثان أ ب هـ ، أ د حـ فيهما:

        ق<1 = ق<2    عملاً

        ق<3 = ق<4    محيطية

        الزاوية الثالثة تكون مساوية للثالثة

        المثلثان متشابهان وينتج أن:

    أ ب     ب هـ

   ـــــــ = ــــــــــ    ومنها أ ب × د حـ = ب هـ × أ د  ... (1)

    أ د      د حـ

    المثلثان أ هـ حـ ، أ ب د فيهما:

        ق<هـ أ حـ = ق< ب أ د    بإضافة < هـ أ د لكل من <1 ، <2

        ق<6 = ق<5    محيطية

        الزاوية الثالثة تكون مساوية للثالثة

        المثلثان متشابهان وينتج أن:

    أ حـ    هـ حـ

   ـــــــ = ــــــــــ    ومنها أ حـ × ب د = هـ حـ × أ د  ... (2)

    أ د      ب د

بجمع (1) ، (2)

 أ ب × د حـ + أ حـ × ب د = ب هـ × أ د + هـ حـ × أ د

                                 = أ د( ب هـ + هـ حـ)

                                 = أ د × ب حـ        المطلوب إثباته