
ريض i253 المسار: ( توحيد المسارات ) صفحة (i1) لاحظ أن أسئلة الامتحان في i5صفحات
مملكة البحرين
وزارة التربية والتعليم
إدارة الامتحانات / قسم الامتحانات
امتحان نهاية الفصل الدراسي الأول للتعليم الثانوي للعام الدراسي i2011/2010
اسم المقرر: الرياضيات i3 المسار: توحيد المسارات
رمز المقرر: ريض i253 الزمـــن: ساعة ونصف
=================================================================================================================
أجب عن جميع الأسئلة الآتية
السؤال الأول: 6 درجات: لكل إجابة صحيحة درجة واحدة
ضع دائرة حول ومز الإجابة الصحيحة في كل مما يأتي:
( i1) ما أبسط صورة للتعبير:

A 3│(x2−5)3│ B │(x2−5)3│ C 9(x2−5)3 D 3│(x2−5)6│
81(x2−5)12i= 34[(x2−5)3]4 :الحـل │

( i3) أي من الدوال الآتية دالة عكسية للدالة ƒ(x)=5x−1 ?
A g(x)=5x+1 B g(x)=1−5x C g(x)=(x+1)/5 D g(x)=1/5x−5 │ الحـل
استبدال موقع x , y أي x = 5 y−1 ومنها y=(x + 1)/5
( i4) إذا كان i24x = 4x+2, فما قيمة x ؟
A 0 B 2 C 4 D 1 الحـل
24x = 22x+4 → 4x = 2x+4 → 2x = 4 → x = 2 │
( i5) التمثيل البياني للدالة (f (x) = log (x−1 هو التمثيل البياني للدالة (f (x) = log (x مزاحاً:
D وحدة واحدة إلى أسفل C وحدة واحدة إلى أعلى B وحدة واحدة إلى اليسار A وحدة واحدة إلى اليمين الحـل
│ التغير في x إلى (x−1) أي وحدة واحدة لليمين فالجواب A
( i6) إذا كان ilog2x2 = 6, فما قيمة x ؟
A −4 B 8 C 2 D 4 الحـل
│ مرفوض log2x2 = 6 → x2 = 26 = 64 → x = 8, x=−8
================================================================================================================
السؤال الثاني: 7.5 درجة الحل
أ ) اكتب log711 في صورة لوغاريتم اعتيادي , ثم أوجد قيمته إلى أقرب جزء من عشرة آلاف. │ log711 = log11÷ log7 = 1.04140 ÷ 0.8451 = 1.2323
===============================================================================
ب ) استعمل log43 ≈ 0.7925 لإيجاد قيمة(log4(3/4 ؟ الحل
│ log4(3/4) = log4(3) − log4(4) = 0.7925 − 1 = −0.2075
=============================================================================
جـ ) إذا كانت المساحة A لسطح مربع معطاة , فإنه يمكن إيجاد ضلع المربع L باستعمال القانون (L = A(1/2 الحل
إذا اشتريت أرضاً مربعة مساحتها i1088 m2, فما طول ضلعها إلى أقرب منزلتين عشريتين. طول ضلعها L = i(1088)1/2 = 32.98
========================================================================================
السؤال الثالث: 11.5 درجة

ب ) إذا كانت ƒ(x) = x − 3 ,ه g (x) = x2 +2 , فأوجد :
( ƒ +g )(x) −1
(ƒ + g )(x) = x2 + 2 + x − 3 = x2 + x − 1 :الحل
( ƒ o g )(x) −2
(ƒ o g )(x) = ƒ[ g (x)] = ƒ[x2 +2] = x2 +2 − 3 = x2 − 1 :الحل
ƒ[(g )(4)]−3
ƒ[(g )(4)] = ƒ[16 + 2] = ƒ(18) = 18 - 3 = 15 :الحل
or ƒ[ g (x)] = x2 − 1 → ƒ[ g (x)] = 16 − 1 = 15 :الحل
==========================================================================================
السؤال الرابع: 13 درجة
( i1) حل كل معادلة مما يأتي :
a) (5 n − 7 )1/3 + 1 = 3
الحل
(5 n − 7 )1/3 + 1 = 3 ينقل 1 للطرف الأيسر ويُطرح من 3
(5 n − 7 )1/3 = 2 بتكعيب الطرفين
[(5 n − 7 )1/3]3 = 23 [2=81/3] بالشكلi2 يمكن تساوي الأساسات بعد وضع
5 n − 7 = 8 بنقل 7 وجمعها مع 8
5 n = 15 بالقسمة على 5
n = 3
b) log60.1 + 2log6x = log62 + log65
الحل
log60.1 + log6x2 = log62×5 قوانين اللوغاريتمات
log60.1x2 = log610 قوانين اللوغاريتمات
0.1x2 = 10 × 10
x2 = 100 الجذر ألتربيعي
x = 10 or [ x = − 10 مرفوض ]
( i2) أنتشر فيروس في شبكة حاسوبية بمعدل i20%من أجهزة الشبكة كل دقيقة . إذا دخل الفيروس إلى جهاز
واحد عند البداية , فأوجد معادلة آسية تمثل انتشار الفيروس منذ البداية .
الحل
A (t) = a(1 + r)t , a = 1 , r = 0.20
A (t) = 1(1 + 0.2)t
= (1.02)t
================================================================================
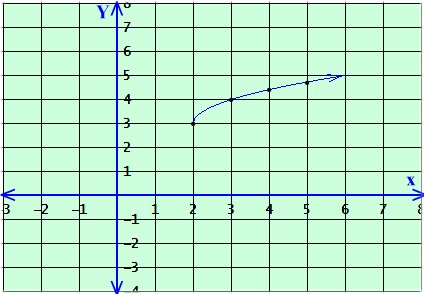 |
السؤال الخامس: 12 درجة أ ) استعمل التمثيل البياني المجاور لدالة الجذر ألتربيعي في إيجاد :
1) قاعدة الدالة .
2) مجال الدالة . { x / x ≥ 2 }
3) مدى الدالة . { y / y ≥ 3 }
ب ) استعمل الدالة y = 2x , للإجابة عن الأسئلة الآتية : أولاً : أكمل الجدول المجاور .
|
||||||||||||
|
|
ثانياً : مثل الدالة بيانياً .
ثالثاً : حدد مجال الدالة . R
رابعاً : حدد مدى الدالة . +R
خامساً : ما نقطة التقاطع مع المحور y ؟ من الجدول أو من التمثيل البياني هي (i(0 , 1
|
=======================================================================================================