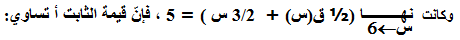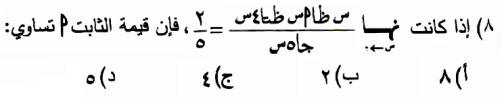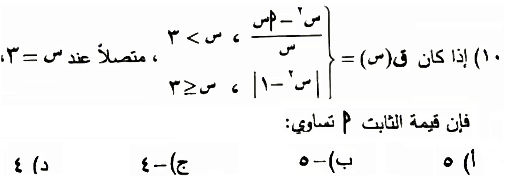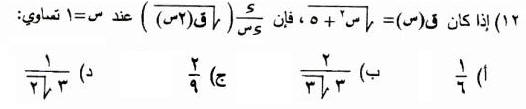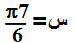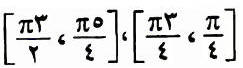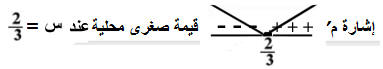|
|
|
|
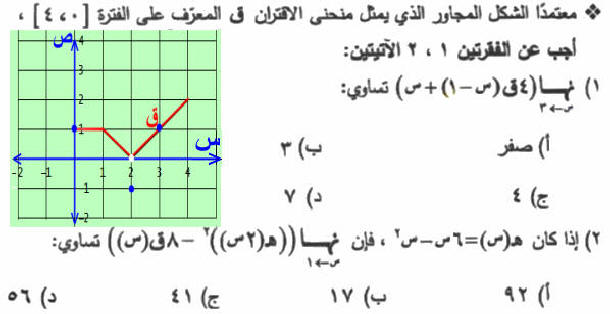
حل 1) نستبدل س - 1 بـ ص، س ¬ 3 فإنّ ص ¬ 3 - 1 = 2 نهــــــــــــا 4 ق(ص) + نهـــــــــــا س= 4 × 0 + 3 = 0 + 3=3 ص ¬2 س ¬ 3
الاجابة الصحيحة ب)
حل 2)
نستبدل 2س بـ ص، س ¬ 1 فإنّ ص ¬ 2 × 1 = 2
( نهــــــا هـ(ص))2- 8 نهـــــــا ق(س) = 28× 1 ص ¬ 2 س ¬1
هـ(2) = 6 × 2 - 4 = 12 - 4 = 8
) نهــــــا هـ(ص))2- 8 نهـــــــا ق(س) = 28-8 =64 -8 = 56
ص ¬2 س ¬1
(الاجابة الصحيحة د)
|
 |
|
حل 3) آخر
المقياس |4 س + 1|وبوضع س =-2 فإنّ 4×-2+1 = -7
قيمة سالبة أي|4 س + 1|=-ه4 س -1=-(4 س+1)ه(
7 -×-(4 س + 1) 8 + 4 س نهـــــــــــــــا ـــــــــــــــــــــــــــــ = ــــــــــــــــــ س ¬ -2 2 س3 + 16 2 (س3+ 8)
4(2 + س) 2 = ـــــــــــــــــــــــــــــــــــــ = ــــــــــــــــــــــــــــــ 2(س + 2)(س2- 2س+4) (-2)2-2×-2+4
2 1 =ــــــــ =ــــــــ 12 6 (الاجابة الصحيحة ج) |
الحــل :
|
|
حــل5): النهاية موجودة ¬ النهاية اليمنى = النهاية اليسرى نهـــــــــــــــا (10 + أ س)2+ = نهـــــــــــــــا (6 - س)+ لكون س سالبة س ¬ 2+ س ¬ 2+ ( 10 + 2 أ )2 = (6 - 2) = 4
10 + 2 أ = 2 أو 10 + 2 أ = - 2
أ = - 4 أو أ = - 6 (الاجابة الصحيحة ج)
================================
حــل7): ميل المماس عند س = 2 هو ق¢(2) = 5 (حاصل ضرب ميلي مستقيمين متعامدين = -1) ق¢(س) = 2 س + ½ هـ¢(س) ق¢(2) = 2 × 2 + ½ هـ¢(س) 5 = 4 + ½ هـ¢(س) ¬ هـ¢(س) = 2 قيمة ½ ق¢(2) - هـ¢(2) = ½ × 5 - 2 = ½ (الاجابة الصحيحة ج) ================================
الحل: ق(س) متصل ¬ النعاية اليمنى = النهاية اليسرى ، النهاية اليسرى = 4 1 حاأس ــ نهـــــــــا(ــــــــــــ)2 = 4 ¬ أ2 = 16 ¬ أ = -4 ، 4 4 س¬0 س (الاجابة الصحيحة أ) ================================
الحل: س2 ق(س)×2س - س2 ق¢ (س) هـ (س) = ــــــــــ ¬ هـ¢ (س) = ــــــــــــــــــــــــــــــــــــــــــــ ... (1) ق(س) ق2(س)
نهـــــــا ق(س) - 2 = 0 ¬ ق(1) = 2 ... (2) س ¬ 1 ق(س) - ق(1) نهـــــــا ــــــــــــــــتـــــــ = 10 ¬ ق¢ (1) = 10 ... (3) س ¬1 س - 1 نعوض في (1) عن س = 1 2 × 2 × 1 - 1 × 10 4 - 10 -6 -3 هـ¢ (1) = ـــــــــــــــــــــــــــــــــــ = ـــــــــــــ = ــــــ = ـــــــ 22 4 4 2 (الاجابة الصحيحة ج) ================================
الحل: لـ 13
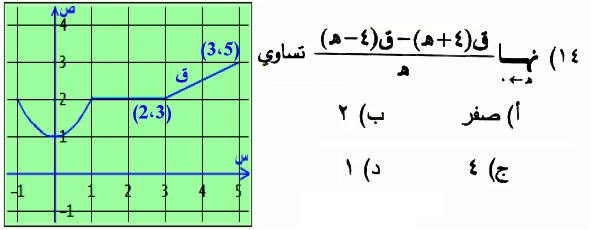
(الاجابة الصحيحة أ) الحل: لـ 14 نضيف ونطرح ق(4) في البسط ونوزع كالآتي:
ق(4+هـ) - ق(4) ق(4) - ق(4-هـ) نستبدل و = -هـ المطلوب = نهــــــا ـــــــــــــــــــــــــــــ + نهــــــا ــــــــــــــــــــــــــــــ هـ ¬ 0 هـ و¬0 و
= ق¢(4) + ق¢(4) =2 ق¢(4) لاحظ ق¢(4) ميل المماس = (3 - 2) / (5 - 3) = ½ =2 × ½ = 1 (الاجابة الصحيحة د) ================================
(الاجابة الصحيحة أ) ================================
الحل: الاتصال: ق(1)+ = 1 + 4 = 5 ق(1)- = 1 + 2 + 2 = 5 ق متصل عند س = 1 فهو قابل للاشتقاق.
2 س + 2 0<س<1 الاشتقاق: ق¢(1) ={ 4 1<س<2
ق¢(1)+ = 4
ق¢(1)- = 2 + 2 = 4 ¬ ق¢(1) = 4
(الاجابة الصحيحة ب) ================================
الحل: -p 1-× p ق¢(س) = ـــــــــــــــــــــ ¬ ق¢(-1) = ــــــــ (1 - س)2 4 (الاجابة الصحيحة د) ================================
الحل: ق/(س) = ن سن – 1 ، ق//(س) = ن(ن – 1) س ن –2 ، ق///(س) = ن(ن – 1)(ن – 2) س ن –3
ق///(س)= جـ س ¬ ن(ن – 1)(ن – 2) س ن –3 = جـ س ألأسس متساوية وكذلك المعاملات أي:
ن - 3 = 1 ¬ ن = 4 ، جـ = 4(4 - 1)(4 - 2) = 4×3×2 ¬ جـ 24 (الاجابة الصحيحة أ)
الحل: بفرض ق(س) = أ س2 + ب س + جـ قاعدة الاقتران المطلوبة ق¢(س) = 2 أ س + ب ... (1) ق″(س) = 2 أ ... (2) في (2): ق″(1) = 2 ¬ 2 أ = 2 ¬ أ = 1 في (1): ق¢(1) = -3 ¬ 2×1×1 + ب ¬ 2 + ب = -3 ¬ ب = -5 في الاقتران المطلوبة : ق(1) = 2 ¬ 2 = 1 × 1 + (-5) + جـ ¬1-5+جـ =2 ¬ جـ = 6
قاعدة الاقتران المطلوبة هي: ق(س) = س2-5 س + 6 (الاجابة الصحيحة ب)
26) إذا كان جتاس = ص2 فإنِّ قيمة ص3(4 ص″ + ص) تساوي: أ) -2 ب) صفر ج) 1 د) -1 الحل: ص2= جتاس بالاشتقاق: 2 ص ص¢ = - حاس
(الاجابة الصحيحة د)
الحل: ق¢(س) = طا(p¼) 2 س + 7 = 1 ¬ س = -3 يالتعويض في معادلة المنحنى: ص = ق(-3) = 9 -21 + 1 = -11 نقطة التماس هي: (-3،-11) (الاجابة الصحيحة ج) ================================
الحل: ع = 8 - 10ن ... (1) ت = - 10 ... (2) 5 (8 - 10ن) = - 10 40 - 50ن = - 10 50ن = 50 ن = 1 ث (الاجابة الصحيحة د) ================================
الحل: ح = س3 بفرض س طول ضلع المكعب س2 = 81 ¬ س = 9 سم نشتق ح بالنسبة للزمن: ح¢ = 3 س2 س¢ ... (1) -24 = 3×81× س¢ ¬ س¢ = -8÷81 م = 6 س2 نشتق: م¢ (معدل تغير المساحة المطلوبة) = 12 س س¢ = 12×9×(-8÷81)
(الاجابة الصحيحة ب) ================================
واضح من الشكل
(الاجابة الصحيحة ج) ================================
================================ حل آخر: بإضافة ±9جتاpس للبسط والتجزئة كالتالي:
================================ السؤال الثاني:ــ
نعرف | س - 10 | = 0 ¬ س = 10 ، سالبة قي الفترة [3 ، 4] أي | س-10|= 10-س ، [(س+1)/2] = 2
عند س =
4: ق(4) =
(س - 4)(س + 4) نهـــــــــــا ق(س)+ = ـــــــــــــــــــــــــــــــ = 8/4 = 2 ... (2) س ¬ 4 4(س - 4)
نهـــــــــــا ق(س)-
=
س ¬ 4
من (1) ، (2) ، (3) ق متصل عند س = 4
عند س =
3: ق(3) =
نهـــــــــــا ق(س) =
س ¬ 3+
من (4) ، (5) ق متصل عند س = 3 من اليمين
ق متصل على مجاله [ 3 ، 6[
================================ السؤال الثاني:ــ
الحـل: ق(ع) - ق(1) ق¢(1) = نهــــــــــــا ــــــــــــــــــــــــــ
س¬1 ع - 1
================================ |
4) إذا كان ق اقتران كثير حدود باقي قسمته على (س - 6) يساوي 2 أ ،
أ) -4 ب) -8 ج) 7 د) 14 الحل: باقي قسمة ق على (س - 6) يساوي 2 أ ¬ ق(6) = 2 أ نهـــــــــا (½ ق(س) + 3/2 س ) = 5 س¬6
¬½× 2 أ + 3/2×6 = 5
أ + 9 = 5 ¬ أ = -4 (الاجابة الصحيحة أ) ================================ 12 6) إذا كان ق اقتران كثير حدود يمر منحناه بنقطة تقاطع المستقيمين ص=ـــــ س، ص=4س-8،
5 وكانت نهــــــــــا ل(س) = -2 ، فإنَّ نهــــــــــا (2ق(2س+1)-3 ل2(س))تساوي: س ¬2 س ¬2
أ) 6 ب) 12 ج) 18 د) 36 الحل: نوجد نقطة التقاطع: َ 4 س-8=12س/5 بالضرب في 5 فإنّ 20س-40=12س ¬8س=40 أي س=5 نعوض لمعرفة ص ، ص = (12÷5)×5 = 12 أي نقطة التقاطع (5 ، 12)
استبدال: 2 س + 1 = ص ، س ¬2 فإنَّ ص ¬ 5
نهــــــــــا (2ق(2 س + 1) - 3 ل2(س)) = نهــــــــــا (2 ق(ص) - 3 ل2(س) ) س ¬2 س ¬2 ص ¬5 س ¬2
= 2 × 12 - 3 × (-2)2 = 24 - 3 × 4 = 24 - 12 = 12 (الاجابة الصحيحة ب) ================================
الحل:
1 × أ 2 ــــــــــــ = ـــــ ¬ أ = 8 (الاجابة الصحيحة أ) 5 × 4 5
الحل: ق(س) متصل ¬ النهاية اليمنى = النهاية اليسرى
(الاجابة الصحيحة ب) ================================
الحل:
الاجابة الصحيحة ب)
================================
================================
الحل: المماس للمنحنى يعني المشتثة تساوي صفر ق¢(س) = - حاس - ½ = 0 حاس = - ½ الزاوية س في الربع الثالث س = p/6 سالبة تعني في الربع الثالث س = p/6 + p
(الاجابة الصحيحة ب) ================================
الحل: -2 لا تنتمي للفترة (-2 ، 2) فإنَّ: ق¢(-2) غير موجودة. (الاجابة الصحيحة د) ================================
الحل: من الشكل المشتقة عند 3 غير موجودة. (الاجابة الصحيحة د) ================================
الحل: ق + هـ هـ(1) ((ق¢(1) + هـ¢(1)) - ((ق(1) +هـ(1))× هـ¢(1) (ــــــــــــ)¢(1)= ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ هـ (هـ(1))2
-1 (2+(-6))-(2+(-1))×-6) -1 (-4)-(1)×-6) = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ = ــــــــــــــــــــــــــــــــــــ (-1)2 1 = 4 + 6 = 10 (الاجابة الصحيحة ب) ================================
الحل: ق¢(س) = جا2س × (- حاس) + 2 جاس جتاس × حتاس = -جا3س + 2 جاس جتا2س
(الاجابة الصحيحة ج) ================================
25) إذا كان ق ، هـ اقترانين قابلين للاشتقاق ، وكان هـ(2) = -½ ، ق¢(-½) = -½ ، هـ¢(2) = -¼ ، فإن (ق o هـ)¢(2) تساوي:
ا) ⅛ ب) -⅛ ج) -¼ د) ¼ الحل: (ق o هـ)¢(2) = ق¢(هـ(2))هـ¢(2) = ق¢(-½)×-¼ = -½×-¼ = ⅛ (الاجابة الصحيحة آ) ================================
(الاجابة الصحيحة ب) ================================
الحل:
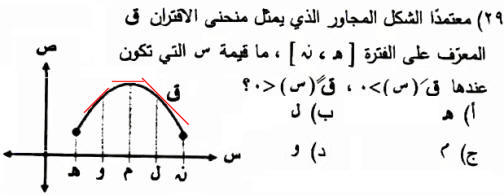
عند الطرفين المشتقة غير موجودة. ق¢(س)> 0 ¬ المنحنى متزايد ، ق″(س)< 0 ¬ المنحنى مقعر لأسفل ، هـ ، ن أطراف فالمشتقة غير موجودة والمماس عند م أفقي فالمشتقة تساوي صفر م مرفوضة عمد ل المماس ميله سالب ق¢(س)< 0 ل مرفوضه عند و المماس ميله موجب ق¢(س)> 0 والمشتقة الثانية ق″(س)< 0 وتقعر المنحنى لأسفل فالجواب هو "و" (الاجابة الصحيحة د)
الحل: مساحة المستطيل (م) = س ص ، ص = ق(س) = س + 5 م = س(س + 5) = س3/2 + 5 س م¢ = 3/2 س× دس/دن + 5 دس/دن معدل التغير في المساحة س = 4 = 3/2 ×2 × 3 + 5 ×3 = 9 + 15 = 24 سم2/د (الاجابة الصحيحة أ) ================================
الحل: ق¢(س) = 2 حاس جتاس ¬ ق¢(س) = 0 ¬ حا س جتاس = 0 حاس = 0 ¬ س = 0 أو س = p جتاس = 0 ¬ س = ½p أو س = p3/2
إشارة ق¢(س)
(الاجابة الصحيحة ج)
================================
الحل:ـ ق¢(س) = 2 حاس جتاس = حا2س ق″(س) = 2 جتا2س ق″(س) = 0 جتا2س = 0 التقعر للآسفل يعني: جتا2س < 0 وهي في الغترات التالية:
(الاجابة الصحيحة أ) ================================
3 - س -1 -4 س ص = ــــــــــــــــــ ¬ ص¢ = ــــــــ ، ق¢(س) = ـــــــــــــــــــــــ 4 4 (س2 + جـ)2 المستقيم يمس المنحنى ¬ ص = ق(س) ، ص¢ = ق¢(س) أي: 3 - س 2 -1 -4 س
4 س2 + جـ 4 (س2 + جـ)2 8
3 - س من (1) في (2): والتعويض 64
9 - 6 س + س2
س - 6 س2+ س3- 4=0
(س - 1)(س2 - 5 س + 4) = 0 ¬ (س - 1) (س - 1) (س - 4) =0
س = 1 ، س = 4 في (1) عن س = 1 : 1 + جـ = 4 ¬ جـ = 3 في (1) عن س = 4 : 16 + جـ = -8 ¬ جـ = -24 مرفوض لأن جـ > 0 أو: نقطة الانعطاف تعني ق″(س) = 0 -4 س
(س2 + جـ)2
(س2 + جـ)2×-4+4 س× 2(س2 + جـ)×2س ق″(س) = ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ (س2 + جـ)4
-4(س2 + جـ)2+8س2(س2 + جـ) ق″(س) = ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ (س2 + جـ)4
-4 (س2 + جـ)+8 س2 ق″(س) = ــــــــــــــــــــــــــــــــــــــــ = 0 ¬ -4 (س2 + جـ)+8 س2= 0 (س2 + جـ)3
س2 + جـ = 2 س2 ¬جـ = 3س2 في (2): (س2 + 3س2 )2 = 16س ¬ 16 س4= 16س 16 س4- 16س = 0 ¬ 16س(س3 -1) 0 ¬ س= 1 أو س = 0 مرفوض لأن س > 0 س= 1 فإن جـ = 3 ================================
س = 0 تهمل ، س = 2/3 ¬ ص = 3 × 2/3 = 2 ¬ أ = (2/3،2) فالنقطة أ(2،2/3) ويكون ميل أ ب = (1-2)/(1-2/3) = 1/(-1/3) = -3 الذي يجعل مساحة المثلث ا ب جـ أقل ما يمكن، ولتحديد القيمة الصغرى فمن م¢ نحدد الإشارة كما مبين بالشكل التالي: (ضع س = 1 (م¢+)، س = 1/3 (م¢-)
================================ |

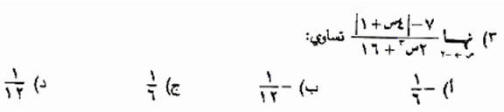

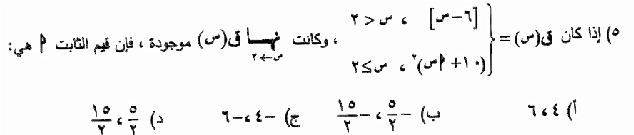


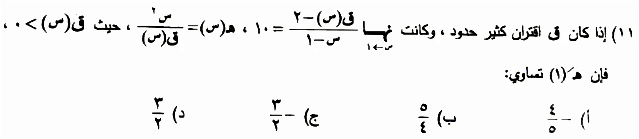





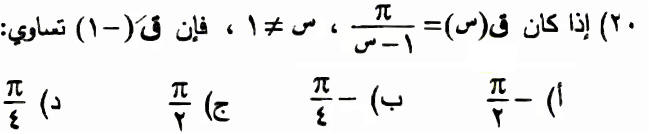








 بالاشتقاق للبسط، المقام
بالاشتقاق للبسط، المقام
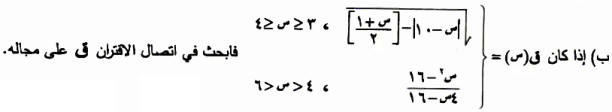

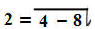 ...
(1)
...
(1)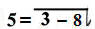 ...
(4)
...
(4)