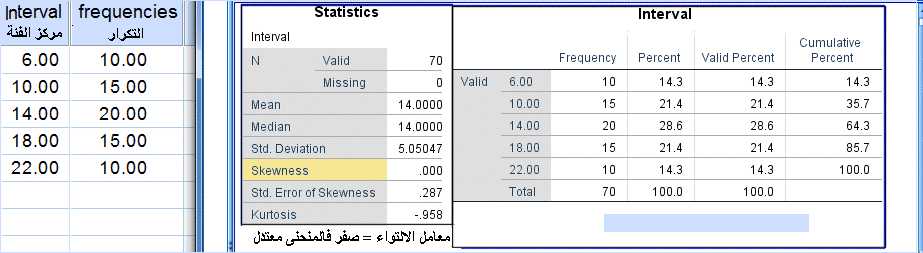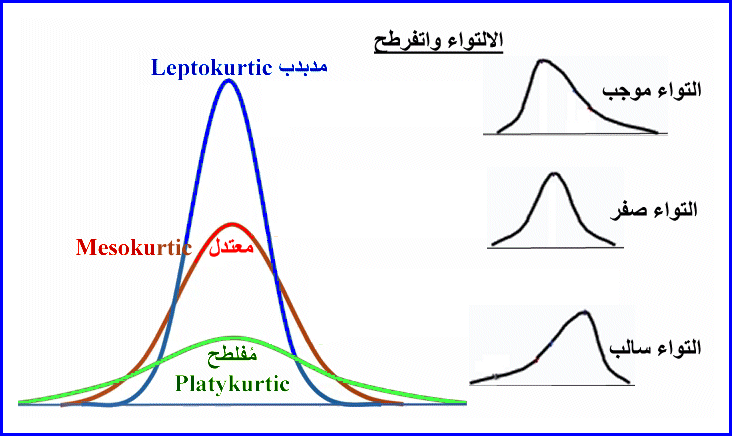
الالتواء والتفرطح:(kurtosis & Skewness)

  إذا كان الوسط الحسابي = الوسيط فالمنحنى التكراري متماثل

    إذا كان الوسط الحسابي > الوسيط فالمنحنى التكراري ملتوي جهة اليمين

    إذا كان الوسط الحسابي < الوسيط فالمنحنى التكراري ملتوي جهة اليسار

 احسب معامل الالتواء من الجدول التالي:

المجموع

24-20

-16

-12

-8

-4

الفئات

70

10

15

20

15

10

التكرار

 

 

 

نوجد الوسط والوسيط والانحراف المعياري ثم يطبق القانون أعلاه.

  
النتائج ح2 × ك ح × ك

الانحراف عن المركز ÷ 4

ح

 مركز الفئة التكرار المتجمع الصاعد

التكرار(ك)

 الفئات

الوسط الحسابي = 14

الوسيط = 14

الانحراف المعياري = 5

معامل الالتواء = صفر

و يعني المنحنى معتدل

40 - 20 - 2 6 10 10 - 4
15 - 15 -1 10 25 15 - 8
صفر صفر صفر 14 45 20 - 12
15 15 1 18 60 15 - 16
40 20 2 22 70 10 24 - 20
110 صفر       70 المجموع

 

By: SPSS

 

لاحظ الآتي:

الانحراف الربيعي = نصف المدى الربيعي      

   P50 = Median   

 Q3 - Q1 = المدى الربيعي

 

 في حالة التوزيع الطبيعي يكون معامل التفرطح المئيني = 0.26 دوما:

ويكون المنحنى للتوزيع مدبدباً حال معامل تفرطحه أكبر من 0.26

ويكون المنحنى للتوزيع مفرطحاً حال معامل تفرطحه أقل من 0.26

 

مثال

مثال: أوجد الالتواء لتوزيع وسطه الحسابي 85 ومنواله 80 وانحرافه المعياري 20 وبين نوعه.

الحل: معامل الالتواء = (الوسط - المنوال) ÷ الانحراف المعياري = (85 - 80) ÷ 20 = 5 ÷ 20 = 0.25 فالالتواء موجب ملتو لليمين

مثال: إذا كان الانحراف الربيعي لتوزيع 30 والمدى المئيني لهذا التوزيع 60 فما نوع التوزيع؟

الحل: معامل التفرطح المئيني = الانحراف الربيعي ÷ المدى المئيتي = 30 ÷ 60 = 0.5 أكبر من 0.26 فالتوزيع مدبب.