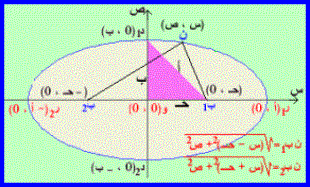
الشكل يمثل قطع ناقص مركزه نقطة الأصل ( 0 ، 0 ) ، ن(س ، ص) إحدى نقطه(الشكل الأول)

ن ب₁ + ن ب₂ = ثابت) من تعريف القطع الناقص)

ن ب₁ + ن ب₂ = 2أ ( بفرض الثابت =2أ ) (1)

حصلنا على ن ب₁، ن ب₂ من قانون البعد بين نقطتين

ومن الشكل بالتعويض عن ن ب₁، ن ب₂ في (1)

[(س– حـ)²+ص²]^½ +[(س+حـ)²+ص²]^½ =2أ

[(س+حـ)²+ص²]^½ =2أ - [(س– حـ)²+ ص²]^½

بالتربيع نحصل على

(س + حـ)² + ص² = 4 أ² – 4أ [(س – حـ) + ص²]^½ + (س – حـ)² + ص²

س²+2 حـ س+حـ²+ص²=4 أ²– 4أ [(س – حـ)² + ص²]^½ + س²-2 حـ س+ حـ² + ص²

- 4أ [(س – حـ)² + ص²]^½ =4 حـ س - 4 أ² بالقسمة على 4

- أ [(س – حـ)² + ص²]^½ = حـ س - أ² بالتربيع

أ² (س²- 2 حـ س + حـ² + ص² ) = حـ² س²– 2 حـ س أ² + أ⁴

أ² س²- 2أ²حـ س+ أ² حـ² + أ² ص² = حـ² س²– 2أ²حـ س+ أ⁴

أ² س² - حـ² س² + أ² ص² = أ⁴ - أ² حـ²

س²( أ² - حـ²) + أ² ص² = أ²(أ² - حـ²) ---(2)

لكن أ > حـ فإن أ²> حـ² أي ( أ² - حـ²) > 0 لاحظ المثلث المظلل

بوضع أ² - حـ² = ب² فتؤول المعادلة (2) إلى (فيثاغورث)

ب² س² + أ² ص² = ا² ب² وبالقسمة على ا² ب²

لاحظ جيداً المحور الأكبر طوله 2أ لذا ا² مقام س² في المعادلة

المعادلة القياسية للقطع الناقص الذي مركزه (0 ، 0) ومحوره الأكبر على محور السينات

بوضع ص = 0 نحصل على س = أ ، س = - أ الإحداثيات السينية لطرفا القطر الرئيسي

بوضع س = 0 نحصل على ص = ب ، ص = - ب الإحداثيات الصادية لطرفا القطر الفرعي

طول القطر الرئيسي(الأكبر) = 2 أ ، طول القطر الفرعي(الأصغر أو الثانوي) = 2 ب

القطع متناظر حول محور الصادات فالمثلث د₁ب₁ب₂ متطابق الضلعين أي 2د₁ب₁=2أ أي د₁ب₁= أ

لأن د₁ أحد أوضاع النقطة ن

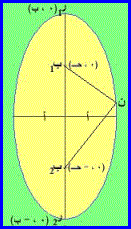
الشكل الثاني البؤرتان على محور الصادات ومعادلة القطع هي

لاحظ وضع المقام في المعادلة فمقام س² للمحور الأكبر بثبات أ، ب، حـ، أ²=ب²+حـ² في الحالتين