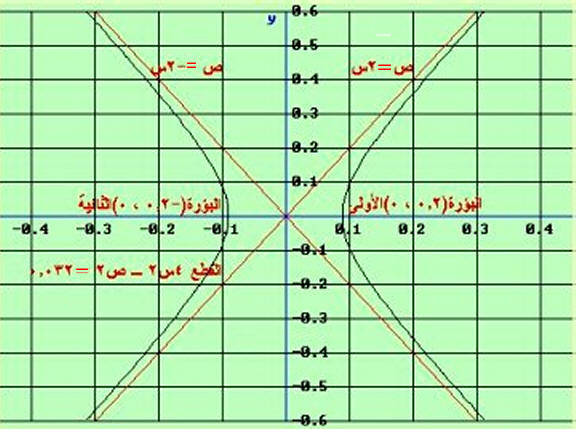
أوجد معادلة القطع الزائد الذي بؤرتاه (± 0.2 ، 0) وخطاه التقاربيان ص = ± 2 س وارسمه
من حيث ألإحداثي الصادي للبؤرة = صفر فإن المحور القاطع للقطع ينطبق على المحور السيني

ومن حيث أن حـ = 0.2 من البؤرة وحيث أن أ2 + ب2 = حـ2 فيكون :
أ2 + ب2 = (0.2)2
أ2 + ب2 = 0.04 ........ (1)
المعادلات التقاربية هي ص = ± ( ب ÷ أ) س
وحيث المعادلات المعطاة ص = ± 2 س يكون ب ÷ أ = 2
ب = 2 أ .......................... (2)
من (2) في (1) نجد أنَّ أ2 + 4 أ2 = 0.04
5 أ2 = 0.04 بالقسمة على 5
أ2 = 1 ÷ 125 وبالتعويض في (2) حيث ب2 = 4 أ2
ب2 = 4 × (1 ÷ 125) = 4 ÷ 125
المعادلة المطلوبة هي :
س2÷ (1 ÷ 125) – ص2÷ (4 ÷ 125) = 1 ×4 ونقل 125 للبسط
500 س2– 125ص2= 4 وهي المعادلة المطلوبة ويمكن وضعها بالشكل
125 س2 – 31.25 ص2 = 1