المعادلات الآتية للقطع المكافئ
(ص –
هـ)2 = ± 4 أ ( س – د ) في حال (د،هـ)=(0،0) فإنَّ ص2 = ± 4 أ س
( س – د )2 = ± 4 أ (ص – هـ) في
حال (د،هـ)=(0،0) فإنَّ س2
= ±
4 أ ص
أي لدينا ثمانية معادلات سنهتم بالحد
المشتمل على س أو ص وليس س2 أو ص2 وهي الأقواس المربعة
فالحد المشتمل على س يعني
المحور موازي محور السينات والحد سالب يعني الفتحة جهة المحور السيني السالب وكونه
حد موجب مع ص يعني الفتحة جهة محور الصادات الموجب ومحوره موازي محور الصادات
ومعرفة هذا يعني لدينا مفتاح الحل. مع ملاحظة أن تكون المعادلة بالصورة المذكورة
أعلاه وإلا يجب تحويلها للصورة أعلاه أن لم تكن كذلك والأمثلة التالية توضح ذلك
![]()
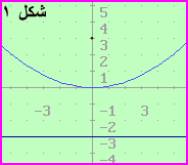
(1) ص2 = 8 س
معادلة
قطع مكافئ رأسه (0 ، 0)
الطرف
الأيسر يحوي س فالمحور موازي محور السينات
إشارة
الطرف الأيسر موجبة فالفتحة جهة اليمين
4
أ = 8 فان أ = 2
البؤرة
هي (أ ، 0) = (2 ، 0 )
معادلة
الدليل هي س = - 2
محور
القطع منطبق على محور السينات
![]()
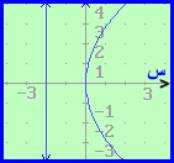
(2) ص2 = - 4 س
معادلة
قطع مكافئ رأسه (0 ، 0)
الطرف
الأيسر يحوي س فالمحور موازي محور السينات
إشارة
الطرف الأيسر سالبة فالفتحة جهة اليسار
4
أ = -4 فان أ = - 1
البؤرة
هي (أ ، 0) = (-1 ، 0 )
معادلة
الدليل هي س = 1
محور
القطع منطبق على محور السينات
![]()
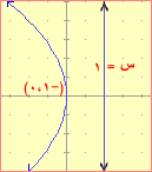
(3) س2 = - 6 ص
معادلة
قطع مكافئ رأسه (0 ، 0)
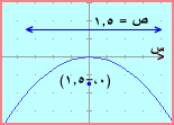
الطرف
الأيسر يحوي ص فالمحور موازي محور الصادات
إشارة
الطرف الأيسر سالبة فالفتحة للأسفل
4
أ = -6 فان أ = - 1.5
البؤرة
هي (0 ، أ ) = (0 ، - 1.5)
معادلة
الدليل هي س = - أ أي س = 1.5
محور
القطع منطبق على محور الصادات
![]()
(4) س2 = 4 ص
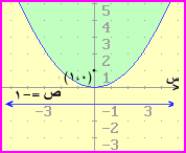
معادلة
قطع مكافئ رأسه (0 ، 0)
الطرف
الأيسر يحوي ص فالمحور موازي محور الصادات
إشارة
الطرف الأيسر موجبة فالفتحة للأعلى
4
أ = 4 فان أ = 1
البؤرة
هي (0 ، أ ) = (0 ، 1 )
معادلة
الدليل هي س = -1
محور
القطع منطبق على محور الصادات
![]()
لمعرفة معادلة القطع يكفي
معرفة قيمة أ فمثلاً والدليل
(1) معادلة القطع الذي بؤرته
(0 ، 3 ) ودليله ص = -3 هي س2 = 4×3س أي س2 = 12 ص
ورأس القطع (0
، 0) ولكن كيف عرفنا ذلك ؟
إذا حددت
البؤرة والدليل على الرسم فالمسافة بين البؤرة والدليل 6 والرأس يقع في منتصف
المسافة بينهما أي (0، 0) والدليل أسفل البؤرة والدليل دوماً خلف القطع المكافئ
لذا فتحة القطع لأعلى والبؤرة واقعة على محور الصادات فمحوره هو محور الصادات ،
كما إن لفظ الدليل بحد ذاته يعني الكلام عن قطع مكافئ لأنه لا دليل في القطوع
الأخرى(الناقص والزائد) كما في شكل1
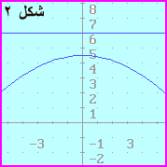
(0 ، 3) غير
كافية لتحديد جهة الفتحة لأعلى أو لأسفل فلو قلنا الدليل هو ص = 6 لأصبحت الفتحة
لأسفل لكون الدليل أصبح أعلى البؤرة وأصبح رأس القطع (0 ، 4.5) لكونه في منتصف
المسافـة بين البؤرة والدليل أي ½
( 0+0 ، 3+6) = (0 ، 4.5) لاحظ أن (0 ، 6) نقطة تقاطع الدليل مع محور الصادات
ومعادلة القطع كما في شكل 2 تصبح
(س – 0)2
= - 4 × 3 ( ص – 4.5) أي
س2
= - 12ص + 54