القطوع المخروطية (ملخص)

·        القطوع المخروطية أربع تنشأ من قطع مخروط دائري قائم ذو قاعدتين بمستو فإن كان:

  • المستوى عمودياً على المحور كان المقطع دائرة.

  • المستوى ليس عمودياً على المحور وغير موازي لراسمه كان المقطع قطع ناقص.

  • المستوى ليس عمودياً على المحور وموازي لراسم فيه كان المقطع قطع مكافئ.

  • المستوى موازياً المحور كان المقطع قطع زائد.

  • والمقصود بالمقطع هو شكل المنحنى الناتج من تقاطع المستوى مع المخروط.

·        المقطع الناشئ ليس تعريفا فالدائرة هي المحل الهندسي لنقطة تتحرك على بعد ثابت

من نقطة أو مجموعة نقاط المستوى التي يتساوى بُعـد كل منها عن نقطة ثابتة فـي

المستوى، النقطة الثابتة تعرف بمركز الدائرة والبعد الثابت يعرف بنصف قطر الدائرة.

  • لسنا هنا بصدد ذكر معلومات عن الدائرة بل سنتطرق للقطوع الثلاثة الأخرى:

المكافئ - الناقص – الزائد، وبصورة مختصرة مفيدة

 

القطـع المكافـئ

            هو المحل الهندسي لنقطة تتحرك في المستوى بحيث يكون بعدها عن نقطة ثابتة في المستوى مساويا بعدها عن مستقيم ثابت في المستوى.

وتعرف النقطة الثابتة بالبؤرة والمستقيم الثابت بالدليل ورأس القطع المكافئ أما أن يكون نقطة الأصل (0،0) أو أي نقطة في المستوى (د ، هـ ) بنقل

المحاور إليها والجدولين الآتيين ملخص عن القطع المكافئ في حالتي الرأس ( 0 ، 0 ) ، ( د ، هـ )

                                         

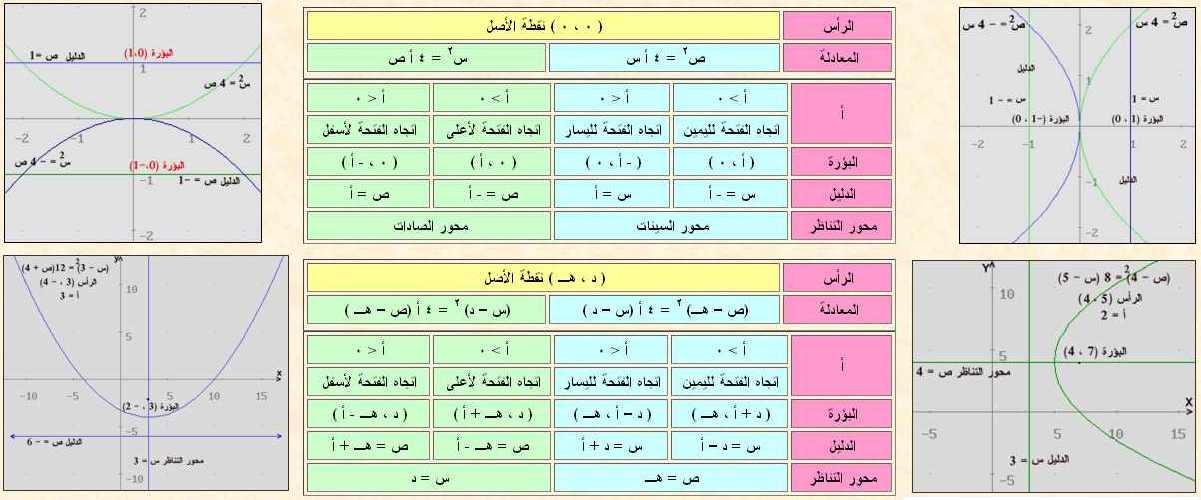
          بعد التقديم السابق يجب الاهتمام بالجدول مع أن الجدول الثاني ناتج من الجدول الأول بنقل للنقطة (د ، هـ) لرأس المنحنى فالعملية هي عملية جمع ، لاحظ البؤرة في الجدول الأول (0 ، أ) أضف (د ، هـ) تنتج البؤرة (د ، هـ + أ) المناظرة في الجدول الثاني وكذلك الدليل في الأول ص = أ وهو الإحداثي الصادي فأضف هـ ينتج ص = أ + هـ وقس على ذلك مع أن هذا ليس علماً بقدر ما هو تسهيلاً إجراء عمل ما ، ومعادلة الدرجة الثانية تؤول بإكمال المربع للصورة القياسية للقطع كما في الصورتين الآتيتين:

الصورة:  س2+ ل س+ ك ص+ ى = 0 هي (س – د )2 = 4 أ (ص – هـ ) حيث ل = - 2 د ، ك = - 4 أ  ، ى = د2 + 4 أ هـ  (1)

الصورة:  ص2+ ل ص+ ك ص+ ى =0 هي (ص – هـ)2 = 4 أ (س – د ) حيث ل = - 2 هـ ، ك = - 4 أ  ، ى = هـ2 + 4 أ د (2)

 إن معرفة د ، هـ ، أ  يعني الحصول على كل ما يتعلق بالقطع المكافئ بما في ذلك الرسم 

مثال : المعادلة ص2 – 10 س + 4 ص – 26 = 0

ص2 + 4 ص = 10 س + 26 بفكرة إكمال المربع لـ ص2 ، 4 ص

            ص2 + 4ص + 4 = 10 س + 26 + 4  إضافة 4 للطرفين

            (ص + 2)2 = 10(س +3) وهي معادلة قطع مكافئ

            رأسه (- 3 ، - 2) ، أ = 2.5 > 0 فالفتحة جهة اليمين

 والبؤرة(- 0.5 ، - 2)

            معادلة محور تناظره ص = - 2

معادلة دليله س = - 5.5 (د – أ)

لاحظ المعادلة ص2 + 4 ص – 10 س – 26 = 0

فمن (2) – 2 هـ = 4 فإن هـ = -2 ، 4 أ = 10 فإن أ = 2.5

، هـ2 + 4 أ د = - 26 فإن د = - 3 وعليه الرأس ( - 3 ، - 2) ، ....

 

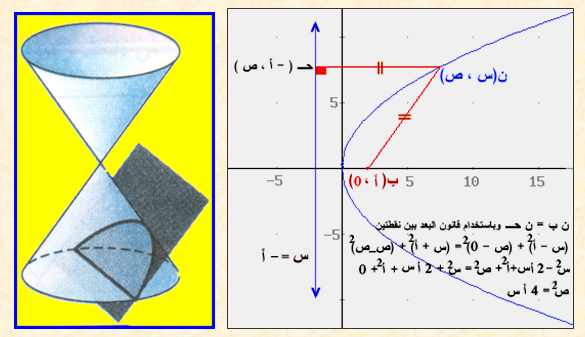
القطع المكافئ نشأته وإيجاد معادلته ص2 = 4 أ س