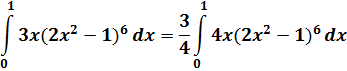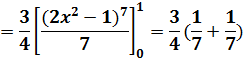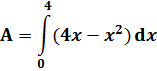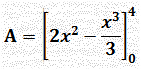الحل مع ملاحظات وغيره

العمود الأيمن نموذج إدارة الامتحانات

قد يتواجد أخطاء فبالإمكان الإبلاغ عنها

Tel. 33686924

المدون في هذا العمود

بواسطة محمد شكري الجماصي

=======================

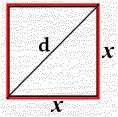
السؤال الأول:

من الشكل المجاور نجد أنَّ :

d² = 2 x² حيث d قطر المربع

A = x² حيث A مساحة المربع

باشتقاق المساحة بالنسبة للزمن

A^\ = 2x x ^\               بالتعويض

0.2 = 2×10x ^\ → 0.1 = 10x ^\

x ^\ = 0.01              معدل الزيادة في طول ضلع المربع

d² = 2x²= 2×100 = 200  لحساب طول قطر المربع

d = 10 √2̅ ,                     طول قطر المربع

d² = 2x² → 2dd^\ = 4x x ^\   بالاشتقاق

2×10√2̅ d^\ = 4×10×0.01             بالتعويض

d^\ = 0.01√2̅  cm/sec     معدل الزيادة في طول القطر

السؤال الثاني:

sin2t = 2sint cost    قانون ضعف الزاوية

s = sin²t                    العلاقة من المسألة 

n =2sint cost (السرعة n =sin2t ) قانون ضعف الزاوية

n │_π/4 =2sin(π/4) cos(π/4)        بوضع t=π/2

          =2(1/√2̅ )(1/√2̅ )

          =2×(1/2)

     n  =1 m/sec                             سرعة الجسيم

ɑ =n ^\ = (2sint cost)^\    ɑ  عجلة الجسيم أو تسارعه

    = 2[sint(  ̶  sint) + (cost)(cost)]

    = 2[ ــ sin²t + cos²t]

ɑ│_π/4 = 2×(  ̶  0.5+0.5) = 0

Or:

n =2sint cost = sin2t →n ^\ = 2cos2t

ɑ│_π/4 = 2×cos(π/2) =2×0 = 0 →ɑ = 0

السؤال الثالث:

بفرض х أحد العددين فإنَّ الآخر هو i40  ̶  хلأن مجموع

العددين i40. ونفرض أنَّ (D(x مجموع مربعي العددين .

أقل ما يمكن يعني D^\(х) = 0  ,  D^\\(х) > 0

D(х) = х² + (40  ̶  х)²  ,  хÎ(0 , 40)

D^\(х) = 2х + 2(40  ̶  х)× ̶ 1

        = 2х  ̶  80 + 2х = 4х  ̶  80

    0  = 4х  ̶  80 → х = 20    أحد العددين

40  ̶  х = 40  ̶  20 = 20              العدد الآخر

D^\\(х) = 4 > 0

 أي مجموع مربعي العددين أقل ما يمكن .

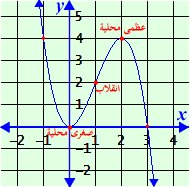
السؤال الرابع:

 ¦(х) = 3х² - х³               نوجد المشتقة الأولى

¦^\(х) = 6х - 3х²        وضع المشتقة الأولى صفر

0 = 3х(2 - х) →х=0 , х=2 عندها نقاط حرجة

х = 0 : ¦(0) = 0 - 0 =0 → (0 , 0) 1نقطة حرجة

х = 2 : ¦(2) =12 - 8=4 → (2 , 4) 2نقطة حرجة

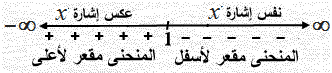
أ) الدالة ƒ متزايدة في [ i[ 0 , 2

          ومتناقصة في ( ¥i(−¥ , 0 ] , [ 2 ,i

 ب) للدالة ƒ قيمة صغرى محلية عند (i(0 , 0(تغيرت إشارة

     الدالة عندها من سالب لموجب).

     للدالة ƒ قيمة عظنى محلية عند (i(2 , 4(تغيرت إشارة

     الدالة عندها من موجب لسالب).

جـ) نوجد المشتقة الثانية ونساويها بالصفر .

¦^\(х) = 6х - 3х² → ¦^\\(х) = 6 - 6х

0 = 6(1 - х)  → х = 1         عندها نقطة انقلاب

 إشارة )х)^\\¦

المنحى ƒ مقعر لأعلى في ( i(−¥ , 1,

          ومقعر لأسفل في ( ¥i [ 1 ,i

х = 1 : ¦(1) =3 - 1=2 → (1 , 2) نقطة انقلاب

 نقاط إضافية لرسم المنحنى

ƒ(−1) = 3 +1 =4      , (−1 , 4)

 ƒ(3) = 27 − 27 = 0  , (3 , 0)   

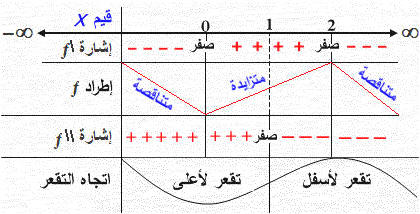
 بالإمكان عمل الجدول الآتي ونستفيد منه في الحل ( التمثيل البياني مطابقاً للمنحنى الموجود في الجدول) .

السؤال الخامس:  لم يعد هذا الموضوع ضمن مقرر ريض 366

الحل مباشرة

                      = (18+3) - (2+1)

                       =18

 السؤال السادس:

أ) الحل يعتمد على تكامل دالة أسية مضروبة في مشتقة أساسها

¦(х) = 2х² - 1 → ¦^\(х) = 4х

خارج القوس i3хفنخرج i3ثم نضرب في i4ونقسم على i4أي :

 ب) نستبدل النص بالإنجليزية ونضرب في مرافق المقام وهو

      (i1 + cosх) ونكمل كالآتي :

حل آخر: نبسط المقام ونستبدل (cosх=1-2sin²(х/2 ونكامل

1 - cosх = 1 - (1 - 2sin²(х/2) = 2sin²(х/2)

1/(1 - cosх) = 1/2sin²(х/2) = ½csc²(х/2)

∫1/(1- cosх)=∫½csc²(х/2)

                   =-½ cot(х/2)

 نفس الجواب السابق  بعد تحويل أياً منهم للآخر .

السؤال السابع: ( كتبنا المعطى بالانجليزية عوضاً عن العربية)

ميل المماس هو المشتقة الأولى وبتكاملها نحصل على معادلة

المنحنى .

m = cos2х =¦^\(х)

¦(х) = ∫cos2х dх

¦(х) = ½ sin2х + c          c ثابت التكامل

  1 = ½ sin2π + c       (π , 1) تحقق معادلة المنحنى

  1 = 0 + c                   sin2π = 0

  c = 1                        بالتعويض

¦(х) = ½ sin2х + 1  

السؤال الثامن:

نوجد نقاط تقاطع المنحنى مع محور السينات وهما حدى التكامل

¦(х) = 4х - х²         ¦(х) = 0 بوضع

     0 = х(4 - х)

 х = 0 , х = 4

A = مساحة المنطقة المحصورة

السؤال التاسع:

* الدالة متصلة في الفترة [i[0 , 2فهي قابلة للتكامل .

* الدالة ليست من الدوال القياسية فيلزم تحويلها لدالة قياسية .

* يتم التعويض عن حدي التكامل , الدالة , dх كالآتي :

х = 0 Þ 0 = 2sinq Þ q = 0

х = 2 Þ 2 = 2sinq Þ 1 = sinq Þ q = ½π

х = 2sinq Þ dх = 2cosq dq