|
العمود الأيمن نموذج إدارة الامتحانات المدون في هذا العمود بواسطة محمد شكري الجماصي قد يتواجد أخطاء فبالإمكان الإبلاغ عنها Tel. 33686924 ======================= السؤال الأول: i1) الإجابة الصحيحة هي C لأنَّ: r = t ‒ 2S = ‹‒ 6 , 2› ‒ ‹8 , ‒ 6 › = ‹‒ 14 , 8 › i2) الإجابة الصحيحة هي C لأنَّ: tan q = y/x = √3̅ /1 = √3̅ q = tan-1√3̅ = 60o i3) الإجابة الصحيحة هي A لأنَّ: AB = B ‒ A = ‹‒ 8 , ‒2, 3› │AB│= √6̅4̅ ̅+̅ ̅4̅ ̅+̅ ̅9̅ = √7̅7̅ i4) الإجابة الصحيحة هي C لأنَّ: P(‒ 1, ‒p/6)=(rcos(‒p/6), r sin(‒p/6)) = (‒ 1√3̅ /2, ‒ 1× ‒1/2) = (‒√3̅ /2 , 1/2) i5) الإجابة الصحيحة هي A لأنَّ: r sinq = r2 cos2q r cos2q بالقسمة على
sinq ــــــــــــــــــــــ = r → r = tanq secq cosq cosq i6) الإجابة الصحيحة هي D لأنَّ: بعد ترتيب القيم تصاعدياً نجد أن Q1 = 4 i7) الإجابة الصحيحة هي A لأنَّ: s =√n̅p̅q̅ , apq = 144×1/6×5/6 =20 s =√2̅0̅ =2√5̅ |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
السؤال الثاني: i1) من الشكل نجد أنَّ:
W2 = V2 + u2 - 2Vucos155o قاعدة الجيب تمام = 102 + 2002 - 2×10×200×-0.9063 = 100 + 40000 +3600 = 43700 W = 209.1 sin 155 ÷ 209.1 = sina ÷ 200 قاعدة الجيب sina = 200 × sin 155 ÷ 209.1 = 0.4042 a = 23.84o أو الحل المقابل
i2) بالتعويض في القانون:
u = W1 + W2 W2 = u - W1
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
السؤال الثالث: i1) بالتعويض في القانون والتبسيط للوصول للجواب.
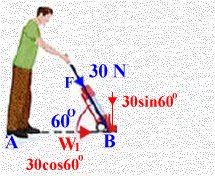
i2) من الشكل بتحليل القوة لنوجد W1
W1 = 30 cos 60o = 30 × 0.5 = 15N
أو بإيجاد احداثيات القوة F بدلالة i30N , 60oوالصورة الإحداثية لمتجه المسافة (i(8,0حيث F = [30cos(-60o), 30sin(-60o)] → W = F . AB = 30×0.5×8 + 0 = 120 J
i3) نوجد حاصل ضرب المتجهين ثم المساحة كالتالي:
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
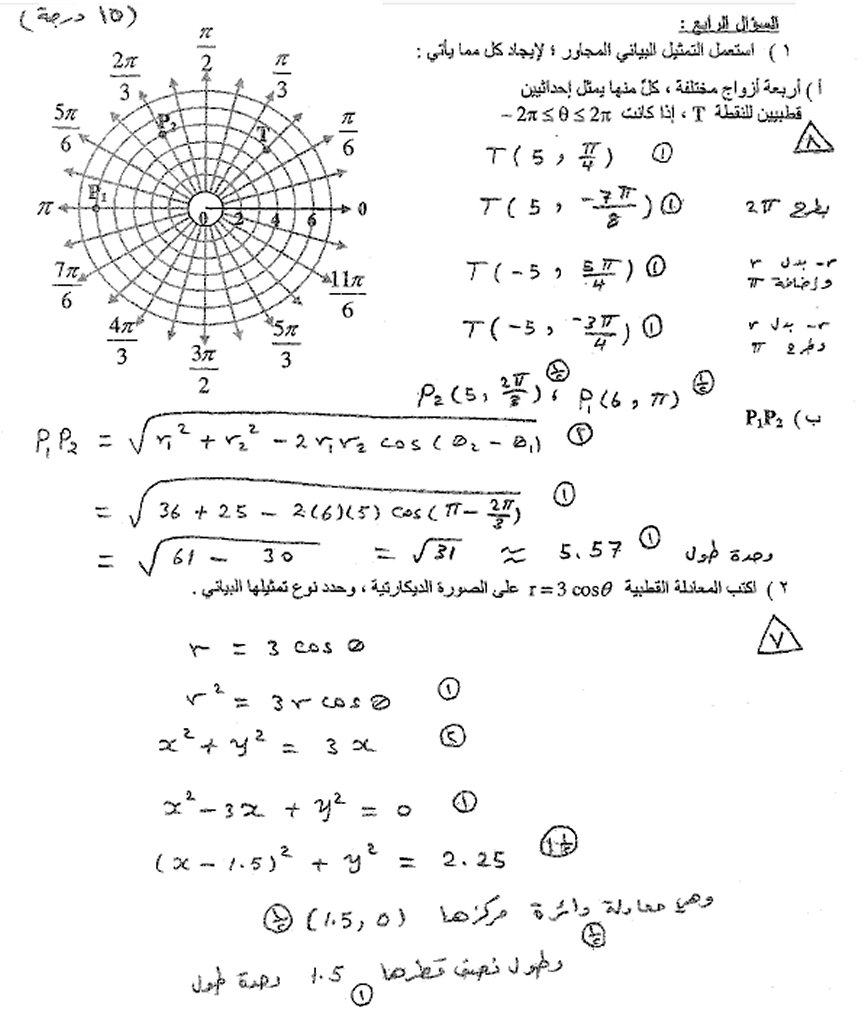
السؤال الرابع: i1) أ) الزوج الأساس هو (T(5 , p/4 والثاني نطرح 2p من p/4 والثالث نطرح p مع تغير إشارة r والرابع نضيف p مع تغير إشارة r .
ب) نكتب القانون والتعويض فالتبسيط فالجواب. p1 = (6 , p) , p2 = (5 , 2p/3)
i2) في الوضع الديكارتي يكون:
(x , y) الصورة الديكارتية , (r , q) الصورة القطبية c = x + y i y وجزئه التخيلي x عدد مركب جزئه الحقيقي r2 = x2 + y2, x = rcosq, y = rsinq , tanq = y/x r = 3 cosq r بالضرب في r2 = 3 r cosq x = r cosq , r2 بالتعويض عن x2 + y2 = 3x بالنقل للطرف الأيمن x2‒3x+y2=0 x بإكمال المربع بإضافة مربع نصف معامل x2 ‒ 3x + 1.52 ‒ 1.52 + y2 =0 نقل للطرف الأيسر (x ‒ 1.5)2 + y2 = 1.52 أي (x ‒ 1.5)2 + (y ‒ 0)2 = 1.52 وهي معادلة دائرة مركزها (i1.5 , 0) ونصف قطرها i1.5 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
السؤال الخامس: i1) نظرية دي ديموافر لأي عدد n صحيح يكون: zn=[r (cosq+i sinq)]n, zn=rn(cos nq + i sin nq) نكتب العدد المركب بالصورة القطبية ومن ثم نستخدم النظرية. r2 = a2 + b2 = (2)2 + 22 = 4 + 4 = 8 , r = 2√2̅ tanq = b ÷ a = 2 ÷ 2 = 1 , q = p/4 2√2̅ (cosp/4+ ¡ sinp/4) الصورة القطبية للعدد المركب هي (2 + 2¡)8 = [2√2̅ (cosp/4 + ¡ sinp/4)]8 = (2√2̅ )8[cos8(p/4) + ¡ sin8(p/4)] = 4096(cos2p + ¡ sin2p) = 4096(1 + ¡×0) =4096(1+0) = 4096 i2) نوجد(P(X=0) , (P(X=1) , P(X=2 والمطلوب ناتج جمعهم أو نوجد (P(X=4) , P(X=5 ونطرح مجموعهم من الواحد الصحيح. P(X=0) = 5C0 (0.45)0 (0.55)5 = 1 ×1×0.5 = 0.5 P(X=1) = 5C1 (0.45)1 (0.55)4 = 5 × 0.45 × 0.0915 = 0.206 P(X=2) = 5C2 (0.45)2 (0.55)3 = 10 × 0.203 × 0.17 = 0.345 المطلوبi= 0.5 + 0.206 + 0.345 = 0.6 ↓أو P(X=3) = 5C3 (0.45)3 (0.55)2 = 0.2757 P(X=4) = 5C4 (0.45)4 (0.55)1 = 0.1128 P(X=4) = 5C5 (0.45)5 (0.55)0 = 0.0185 المطلوبi=1 ̶ [P(X=3)+P(X=4)+P(X=5)] =1 ̶ (0.2757 + 0.1128 + 0.0185) = 1 ̶ 0.4070 = 0.6 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
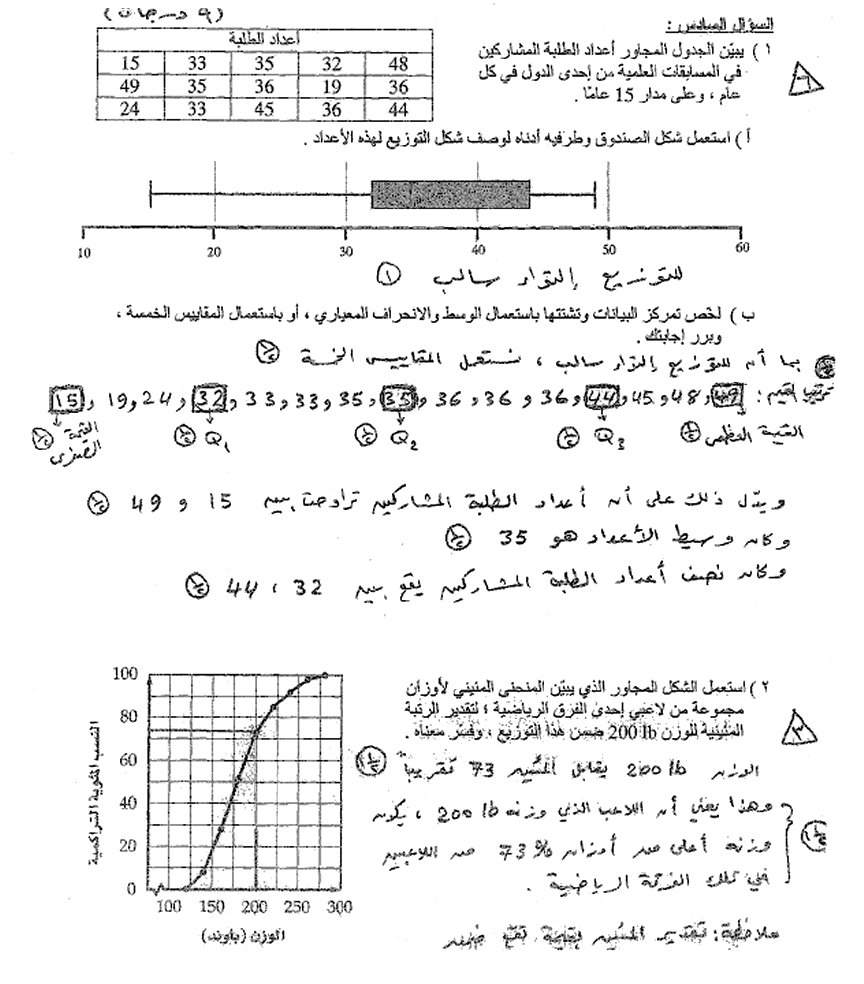
السؤال السادس: i1أ) للتوزيع التواء سالب لأن الجهة يمين الوسيط أطول من يساره i1ب) نستعمل المقاييس الخمسة لأن للتوزيع التواء سالب. ترتب القيم تصالعدياً : 15, 19, 24, 32, 33, 33, 35, 35, 36, 36, 36, 44, 45, 48, 49 المقاييس الخمسة 15 القيمة الصغرى 49 القيمة العظمى 32 Q1 الربيع الأول 44 Q3 الربيع الثاني 35 Q2 الوسيط * واضح أن أعداد الطلبة تراوحت بين i15 , 49 * نصف اعداد الطلبة يقع بين i32 , 44
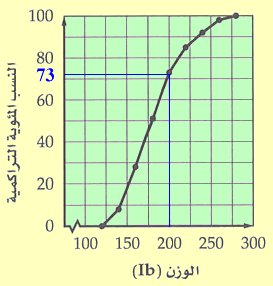
i2) بإقامة عمود من i200يلاقي المنحنى في نقطة نرسم منها خط يوازي المحور الأفقي يلاقي محور النسب عند i73تقريباً ويدل على أن اللاعب ذو الوزن i200 Lbيكون أعلى من أوزان i73%من لاعبي الفرقة الرياضية.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
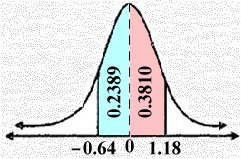
السؤال السابع: نحول الدرجات المعطاة قيم Z لحساب المساحة تحت المنحنى X = 65: Z = (X ̶ m)/s = (65 ̶ 72)/11 » ̶ 0.64 X = 85: Z = (X ̶ m)/s = (85 ̶ 72)/11 » 1.18 من جدول Z المرفق نجد أنَّ:
المساحة المقابلة للقيمة Z = ̶ 0.64 تساوي i0.2389 المساحة المقابلة للقيمة Z = 1.18 تساوي i0.3810 تكون نسبة الدرجات الواقعة بينi65 , 85 تساوي المجموع أي المطلوب = i0.2389 + i0.3810 = i0.6199 » 0.62 أوi 62% |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
جزء من جدول Z يفي بغرض المسألة - هنا الجدول كامل
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||