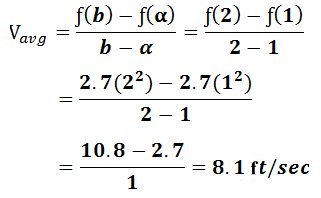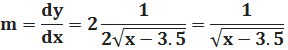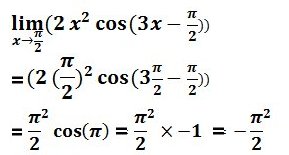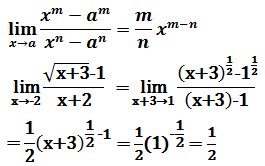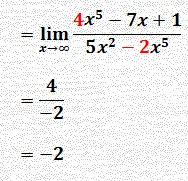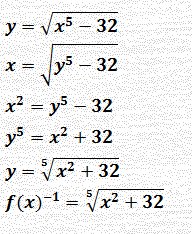الحل مع ملاحظات وغيره

العمود الأيمن نموذج إدارة الامتحانات

Tel. 39910300

المدون في هذا العمود

بواسطة محمد شكري الجماصي

قد يتواجد أخطاء فبالإمكان الإبلاغ عنها

=======================

السؤال الأول:

i1) الحل يعتمد على العلاقات الآتية :

1 + tan²q = sec²q → sec²q  ̶  1 = tan²q

tanq cotq = 1 , (x + y)(x  ̶  y) = x²  ̶  y²

i2) متوسط السرعة لجسم لفترة زمنية من α إلى b هي :

    حيث موقع دالة الجسم في الزمن هو (t¦(tنعوض عن قيمتي

    الزمن حيث a = 1 , b = 2 ونوجد متوسط السرعة

 i3) ميل المماس هو المشتقة الأولى, مشتقة الجذر التربيعي هي

      كسر مقامه ضعف الجذر وبسطه مشتقة ما بداخل الجذر .

                       الإجابة صحيحة

إذا كانت y = 2x  ̶  3.5  كما جرى تعديله في نص المسألة فإنَّ:

 i4) ننقل المقام للبسط مع تغير أشارة الأس ومن ثُمَ نكامل .

¦(z) = 12z ^{̶  3}  ,  F(z) = ∫¦(z)dz = ∫12z ^{̶  3} dz

       = (12z ^{̶  2}÷ ̶ 2)+c= ̶ 6z ^{̶  2}+c =  ̶ 6/z² + c

السؤال الثاني:

i1) التعبير هنا هو ناتج (tan(59^o - 14^o أي tan45^o حيث :

 tan45^o = 1  ,

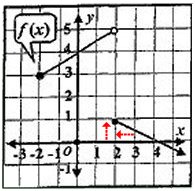
i2) كلما اقتربت x من جعهة اليمين للعدد i2فإن قيم الدالة تقترب

 من العدد i1كما يبينه الشكل المرفق .

i3) عند النقطة x = c

  انفصال قفزي : وجود نهاية يمني ويسرى ولكنهما غير

                     متساويتين. (هذا موجود في الشكل المرفق).

  انفصال لانهائي : تزايد قيمة الدالة بلا حدود عند اقتراب

                          x من c من اليمين أو اليسار .

  انفصال نقطي : تكون الدالة متصلة عند كل نقطة بمجالها

                    عدا النقطة x = c                    

i4) نوجد (g(1  وناتجه i2ونوجد (f(2  والناتج i2أو الآتي :

[¦og](1) = ¦(g(1)) = ¦(√1̅+̅3̅ ) = ¦(√4̅ )

              = ¦(2) = 2² - 2 = 4 - 2 = 2

i5) الدالة الأم تُزاح أما أفقياً أو رأسياً أو كلاهما فالتغير في х

     ألى (х+2) إزاحة بقدرi2لليسار , (المحور السيني السالب)√

     ألى (х-2) إزاحة بقدرi2لليمين , (المحور السيني الموجب)

     ألىi¦(х)+3iإزاحة بقدرi3لأعلى (المحور الصادي الموجب)

     ألىi¦(х)-3iإزاحة بقدرi3لأسفل (المحور الصادي السالب)

i6)  

 α –(α) = 8 → 2α = 8 → α=4

i7) الخط الرأسي يقطع المنحنى في نقطة واحدة فقط ليكون

     التمثيل البياني يمثل دالة , وهذا متوفر في الشكل B √

السؤال الثالث:

i1) نسند الزاوية i67.5^oلزاوية أخرى والأنسب هنا i135^o

     ونستخدم العلاقة المثلثية :

  نعوض عن q والحل:

i2) نضرب حدي الكسر في qsin ونستخدم العلاقات الآتية :

sinq cscq =1  i1 = لنسبة × مقلوبها

cos²q = 1 − sin²q = (1 − sinq)(1 + sinq)

sinq = RHS

لاحظ الحل المقابل

i3) نستخدم العلاقات المثلثية الآتية :

sin2q = 2sinq cosq

sin2q tanq = 3sinq + 2

2sinq cosq sinq ÷ cosq = 3sinq + 2

2sin²q - 3sinq - 2 = 0

(2sinq +1)(sinq -2) =0

2sinq + 1 = 0 or  sinq-2 = 0  مرفوض

sinq = - 0.5 → تقع في الريع الثالث أو الرابع q

قيمة الزاوية  i210^o أو i330^oوبالتقدير الدائري

الحل العام نضيف i2Kp

sinq ϵ [ -1 , 1 ]

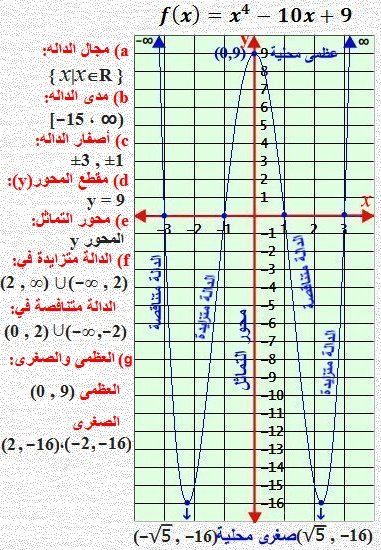
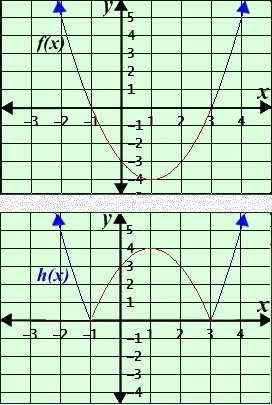
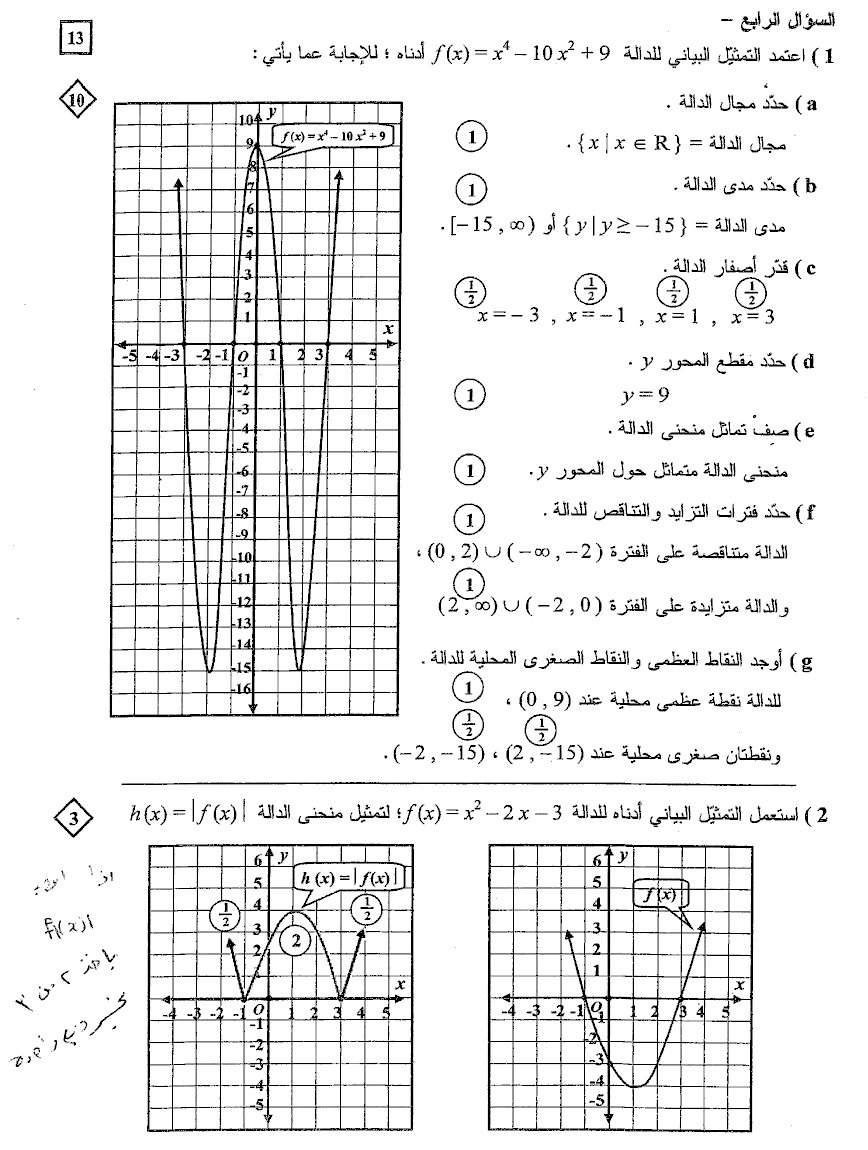
السؤال الرابع:

i1) الشكل الآتي تمثيل بياني للدالة المبينة ولا علاقة له بالآخر

i2) دالة المقياس موجبة دوماً فنعكس الجزء السالب في محور х

¦(х) =х² - 2х - 3    ,     h(х) =│¦(х)│

السؤال الخامس:

i1) نتبع الآتي: التوزيع ـ تعويض مباشرة عن x ـ cosp=-1

i2) عندما يكون ناتج التعويض المباشر (i0 ÷ 0) نجري تحليل

      للتخلص من الكمية التي تنتج هذا وهي هنا x + 2  لاحظ ما

      تؤؤل إليه x ووجود الجذر يعني الضرب بالمرافق سواء كان

      موجوداً في البسط أو المقام أو كلاهما حيث مرافق البسط هنا

х→-2 → х+2→0

OR

i3) عندما يكون ناتج التعويض المباشر (∞÷∞) نقسم

     على المتغير الذي له أكبر أس أي x⁵ حيث :

وناتج النهاية (درجة البسط = درجة المقام = 5) يساوي معامل أكبر أس في البسط مقسوم على معامل أكبر أس في المقام فهنا المعاملات هي i4 , -2, وبناء على ذلك يكون الحل كالآتي :

السؤال السادس:

i1) لإيجاد الدالة العكسية :

     * نضع (y = ¦(х

     * نستبدل х بـ y , y بـ х

     * نحسب قيم y بدلالة х

     * نستبدل y  بـ i¦(х)^-1 

i2) *  يكتب التعريف أو خطوة خطوة للزصزل للتعريف

     *  التعويض

     *  الجواب

     *  التعويض عن قيمة x .

¦(х) = х² + 8

¦(х+h) = (х+h)² + 8 = х² + 2хh + h² + 8

¦(х+h) - ¦(х) = х² + 2хh + h² + 8 - х² - 8

                       = 2хh + h²

                       = h(2х + h)

¦(х+h) - ¦(х)      h(2х + h)

—————— = ————

         h                     h

¦(х+h) - ¦(х)

—————— = 2х + h

         h

       ¦(х+h) - ¦(х)

lim  —————— = lim (2х + h) = 2х

h→0         h               h→0         

¦^/(х) = 2х

¦^/(½) = 2×½

        = 1

السؤال السابع:

i1) *  نوجد المشتقة الأولى .

     *  نساوي ^\(х)¦ بالصفر, الكسر = صفر فبسطه صفر .

     *  نوجد قيم المتغير х وعندها النقاط الحرجة .

     *  نعوض عن قيم х في الدالة الأصلية لحساب y .

     *  نكتب النقاط .

(5 , 0.1) , (-1 , 0.5)  النقاط الحرجة هي

i2) *  المسافة تساوي تكامل السرعة

     *  نوجد قيمة ثابت التكامل C بوضغ S = 1000 , t = 0

     *  لحساب زمن الوصول للأرض نضغ المسافة تساوي صفر

a) s(t) = ∫v(t)dt = ∫-50t dt = -½×50t ² +c

      = -25t ² + c       t = 0 عند الزمنi100  المسافة

1000 = -25×0 + c

c = 100

b) s(t) =-25t ²+100  بوضع المسافة = صفر لحساب الزمن

0 = -25t ² + 100

25t ² = 100 → t ² = 4 → t = 2 sec

السؤال الثامن:

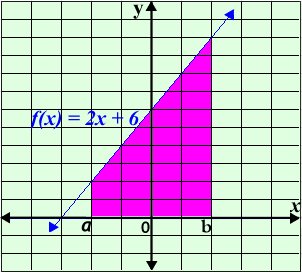
i1) التكامل ثم التعويض

i2) نستخدم قانون حساب المساحة بالتكامل (طريقة ريمان)

     أو التجزيء النوني المنتظم في ريض i317

للتأكد: نحسب مساحة شبه المنحرف (المنطقة المظللة) ولتكن A

 A= 0.5(2+10)×4 = 0.5×12×4 = 24  وحدة مساحة

مساحة شبه المنحرف = ½ مجموع قاعدتيه المتوازيتن × الارتفاع

وهذا ليس بحل فقط للتحقق