أجب عن جميع أسئلة هذا الامتحان وعددها i7                                                            الدرجة النهائية i100

 i20 درجة  لكل فقرة

i1) مضاعفات العدد هي مجموعة الأعداد الناتجة من ضربه

      بالاعداد الطبيعية ... _وi1, 2, 3, 4 فمضاعفات i8هي

      8×1, 8×2, 8×3, .... أيi8n, nÎN صحيحة B فتكونة

i2) أصفار الدالة تنتج من وضع g(X) = 0

 g(X)=2X (X² − 1) = 2X(X − 1)(X + 1)

 g(X) = 0 → X  = 0 , X  = 1 , X = −1  

i3) بتبسيط الدالة ƒ ومن ثُمَ إجراء القسمة ثُمَ التعويض.

   ƒ(X) = 6X ² − 15X = 3X(2X − 5) , g(X) = 3X

   ƒ(X) ÷ g(X) = 2X − 5

    ƒ

 (—﴿(5) = 2 × 5 − 5 = 10 − 5 = 5

    g

 i4) متوسط معدل التغيّر للدالة في الفترةi[ X₁ , X₂[i هو:

                 g(X₂ ) − g(X₁ )

m_sec= ———————         وبالتعويض نحصل على 

                    X₂  − X₁ 

           ——     —                      ———    —

g(2)=√2 +7=√ 9 =3 , g(−3)=√−3+7 =√ 4 = 2

  g(2 ) − g(−3 )       3 − 2       1

 ——————  = ——— = —

      2  − (−3)              2 + 3         5

 i5) لمعرفة الإجابة يجب معرفة الرسم البياني لهذه العلاقات

  أو اذا النقطة (x, y) واقعة على المنحنى فإن النقطة (x, −y)

  واقعة عليه. وهذا صحيح مع العلاقة في A فقط

i7) تكون الدالة فردية إذا كان: ( ƒ(−X) = − ƒ(X أو تكون

     الدالة متماثلة حول نقطة الأصل أي إذا كانت النقطة (x , y)

     واقعة على المنحنى فإنَّ النقطة (x , ^_ y^_) واقعة عليه.

      وهذا محقق في A

i8) المساحة تحت المنحنى = i1

i9) الدالة الأصلية هي تكامل الدالة ^½ƒ(x) = 3x وتساوي

   F(x) = (⅔)×3x^(3/2) + C

= 2x^3/2 + C

 — 

=2√x³ + C

i10) المدى الربيعي هو الفرق بين المدى الربيعي الثالث والأول

 i15 درجة  (i1) ثمانية , (i2) سبعة

i1) من الشكل نجد أنَّ:

 a) مجال الدالة [ i−∞ , 3) ، مداها [ i ( −∞ , 2

 b) مقطع المحور y هو:  y = −2

 c) الدالة متزاية في: (i(−∞ , −2) , (i0 , 2

     والدالة متناقصة في: (i(−2 , 0)i, (2 , 3

 d) للدالة قيمة عظمى محلية عند X = −2 , X = 2

     للدالة قيمة صغرى محلية عند   X = 0

i2) نثبت أنَّ  (ƒ o g)(x) = (g oƒ)(x)

  نوجد (g oƒ)(x) نجدها x , ونوجد (ƒ o g)(x) نجدها x

أو نضع ƒ(x) = y ونبدل أماكن x , y ونكرر ذلك للدالة الأخرى

        i2                         2

  y = — x + 3  → x = — y + 3 → 2y = 5x − 15

         5                        i5    

                                   5

 2y = 5(x − 3) → y = — (x − 3) = g(x)

                                   2

        i5                        5

  y = —(x−3) → x = —(y − 3) → 5y= 2x + 15

         2                       i2    

 نقسم على i 5

         2

  y = — x + 3 = ƒ(x)       كلا من الدالتين عكسية للأخرى

         5

i11 درجة  ( i1) خمسة , ( i2) ستة

i1) طريق الحل:

     *  نكتب التعريف

     *  نعوض

     *  نبسط الناتج

     *  نأخذ النهاية

i2) متشقة الدالة النسبية هي:

                المقام × مشتقة البسط − البسط × مشتقة المقام

  المشتقة = ———————————————

                                  مربع المقام

    نوجد مشتقة البسط

    نوجد مشتقة المقام

    نعوض في متشقة الدالة النسبية (أعلاه)

    نبسط الناتج

    الجواب

i15درجة: (i1a)ثلاثة,(i1b)ثلاثة,(i3a)أربعة,(i3b)خمسة

i1) حساب النهايات:

                    X  − 1            −2 −1        −3        

a ) lim ————— = ———— = — = −1  

                     ———        ———        3

      X→−2   √X + 11        √−2+11        

            X ² −3X −10              (X −5)(X +2)

b ) lim  —————— = lim  ——————

    X→5       X − 5            X→5        X − 5  

    = lim (X + 2) = 5 + 2 = 7

      X→5

   a ) ∫( 24X ⁷ − 4X ⁻⁵  + 13) dX

          24X ⁸    4X ⁻⁴

     = —— − ——— +13X + C

            8         −4

  = 3X ⁸ + X ⁴ + 13X + C

       2 

  b )  ∫ (3X ² − 4X + 5 ) dX

    0

                                   2                              2  

    =│3X ³       4X²  + 5X│=│ X ³ −2X ² + 5X│

            ——  − ——

               3            2                0                                      0

    =( 8 − 8 + 10) − (0) = 10

i10 درجة  ( ia) درجتان , ( ib) ستة , ( ic) درجتان

a) من الشكل الآتي:

     Q₁ الرُبيع الأول , Q₃ الرُبيع الثالث

   حددنا في الشكل المقاييس الخمسة لكون التوزيع ملتو جهة

   اليمين أي التواء موجب.

i13 درجة  ( ia) أربعة , ( ib) درجتان , ( ic) سبعة

a) التمثيل البياني للجدول

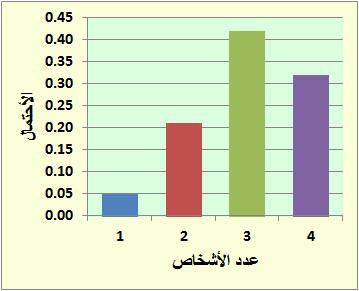
c) الوسط : μ = n p أو [(μ = ∑[X . P(X

    التباين : σ² = n p q أو [(σ² = ∑[(X−μ)^{2 .} P(X

    المتغير العشوائي X = 1 , 2 , 3 , 4

 n = 4 , p = 0.75 , q = 1 − 0.75 = 0.25

μ = ∑[X . P(X)]      ( 3.01 من الجدول)

    = 1 × 0.05 + 2 × 0.21 + 3 × 0.42 + 4 × 0.32

    = 0.05 + 0.42 + 1.26 + 1.28 = 3.01 ≈ 3

σ²= ∑[(X−μ)^{2 .} P(X)]    ( 0.73 من الجدول)

    = (1−3)² × 0.05 + (2−3)² × 0.21 + (3−3)²×0.42 +

        (4−3)²×0.32

     = 4 × 0.05 + 1 × 0.21 + 0×0.42 + 1×0.32

     = 0.20 + 0.21 + 0 + 0.32 = 0.73

i16درجة: a) سبعة , b) تسعة

a) نحسب Z من القانون , ومن جدول Z المساحة تحت المنحنى

b) نحسب Z لكل من القيمتين i175, 226ثم نحسب المساحة كما

     مبين بالشكل

السؤال الأول:

اختر رمز الإجابة الصحيحة في كل مما يأتي , علماً بأنه لا توجد سوى إجابة صحيحة واحدة لكل فقرة :

i1) ما الصفة المميزة لمجموعة اعداد المضاعفات الموجبة للعدد i8؟

     X \ X = n + 8 , n Î N }    C                       { X \ X = 8ⁿ , n Î N }    A }

{ X \ X = n − 8 , n Î N }    D                       { X \ X = 8n , n Î N }    B ü

i2) ما أصفار الدالة  g(X) = 2X³ − 2X  

{ 0 , 1 , 2 }   C                     {i0 , −1 , 1 }    A ü

     i−2 , 2 }    D                     {i0 , −2 , 2 }    B}

                       ƒ

i3) ما ناتج ( i5)﴿—) للدالتين  g(X) = 3X  ,  ƒ(X) = 6X² − 15X

                       g

     C                                  −15    A ه i0    

     i 5   D ü                              −5     B

                                             ——

i4) ما قيمة متوسط معدل التغيّر للدالة  g(X) =√X +7 في الفترة [ i−3 , 2]

                                                                            i1

      C ü                                −1    A  ه  —    

                                                                            i5

                i1

      D                                − —    B  ه   i1    

                i5

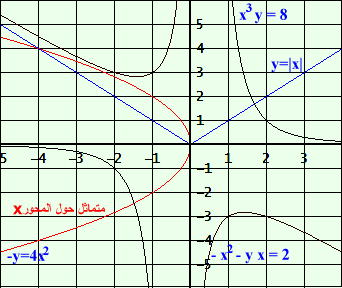
i5) أي من العلاقات الآتية متماثلة حول المحور X ?

y = | x |    C                     −y² = 4x     A ü    

             −x² − y x = 2    D                       x³ y = 8     B         

i6) ما ميل المنحنى ƒ(X) =X ² + 1 عند النقطة ( i2 , 1)

     C                                  1     A ه  i3    

     i 4   D ü                              2     B

  الحل

    نوجد المشتقة الأولى ثم نعوض:

 ƒ^\(X) = 2X

        ƒ^\ (2) = 2×2       

       = 4

i7) أي من الدوال الآتية فردية ؟

ƒ(X) = 3 X ² − 4X ² + 4    C                             ƒ(X) = X ³ − 4X     A  ü

 ƒ(X) = X ² − 4    D                      ƒ(X) =2 X ³ + X ² −X    B      

   الحل

    ( ƒ(−X) = −X ³ + 4X =−(X ³ − 4X) =−ƒ(X

i8) إي مما يأتي ليس من خصائص التوزيع الطبيعي ؟

 A      i   الوسيط − الوسط − المنوال                     و i C  يقترب المنحنى من المحور X ولا يمسه

        B   المنحنى متصل        و                       ü اD     المساحة تحت المنحنى > i1

                                    —

i9) ما هي الدالة الأصلية للدالة  ƒ(x) =3√x ؟

           3 —                                        —

F(x) = √x² + C          C        F(x) = √x³ + C        A

              3—                                        —

F(x) = 2 √x² + C       D        F(x) =2 √x³ + C       B ü

i10) يبين المنحنى المئيني المجاور درجات طلاب إحدى المدارس

       في أحد مختبارات المحاسبة. ما الرتبة المئينية للدرجة i44?

        i 80   C ü                      i40   A  

        i 70   B         و               i90   D

       من القيمة i44على محور الدرجات نرسم خط رأسي يلاقي

       المنحنى في نقطة , ومنها نرسم خط أفقي موازي محور

       درجات الطلاب فيلاقي المحور الرأسي عند القيمة i80وهي

       الرتبة المئينية للدرجة i44.

       فالإجابة الصحيحة C .

السؤال الثاني:

i1) اعتمد التمثيل البياني للدالة h المجاور ؛ للإجابة عما يأتي :

     a) حدد مجال الدالة h , مداها .

     b) حدّد مقطع المحور y .

     c) أوجد فترات التزايد والتناقص للدالة .

     d) قدّر الاحداثي X للنقاط العظمى والصغرى المحلية للدالة .

               i5                            2

i2) أثبت جبرياً أن كلا من الدالتين g(x) = — (x − 3) , ƒ(x) = — x + 3 دالة عكسية للأخرى .

                    2                           i5    

       الحل:

             نثبت أنَّ  (ƒ o g)(x) = (g oƒ)(x)

                                    5                2   5

(ƒog)(x) = ƒ(g(x) = ƒ[(−(x−3)] = −(−(x−3)) + 3 = x −3 + 3 = x

                                    2                5   2

                                 2             5    2

(goƒ)(x)=g(ƒ(x))=g[(−x+3)]=−[(−x+3−3]=x

                                 5             2    5

(ƒ o g)(x) = (g oƒ)(x) = x

            إذن كلا من الدالتين ƒ , g دالة عكسية للأخرى .

السؤال الثالث: 

i1) باستعمال التعريف أوجد مشتقة الدالة ƒ(X) = 4X − 5

                            ƒ(X + h) − ƒ(X)             [4(X + h) − 5] −[(4X − 5)]       

   ƒ^/(X) = lim ——————— = lim —————————————                                  الحل 

                  h→0              h                  h→0                     h                                  

                                                               4X + 4h − 5 −4X + 5

                                                 = lim ——————————

                                                                h→0                   h

                                                                4h

                                                 = lim  —— = 4

                                                                h→0     h

i2) أوجد مشتقة الدالة ( ƒ(W عند iW = 4 حيث

     الحل

W² + 8

    ƒ(X) = ———   ,  X  ≠ 2

W − 2

h(X) = W² + 8   →   h^/(X) = 2W       البسط ومشتقته

g(X) = W −2 →  g^/(X) = 1             المقام ومشتقته

                (W −2)×2W − (W² + 8)×1        2W ² −4W −W ²  − 8         W² − 4W  − 8      

 ƒ^/(W) = ——————————— = ————————— = ——————

                               (W − 2)²                          (W − 2)²                   (W − 2)²

                4² − 4 × 4  − 8      16−16 −8       −8

 ƒ^/(4) = ——————— = ————— = —— = −2

                      (4 − 2)²                       4                4

السؤال الرابع: 

i1) احسب كل  نهاية مما يأتي , أن أمكن :

                    X  − 1  

a ) lim —————

                     ——— 

     X→−2   √X + 11  

            X ² −3X −10

b ) lim  ——————

    X→5       X − 5       

i2) احسب تكامل كل مما يأتي :

a ) ∫( 24X ⁷ − 4X ⁻⁵  + 13) dX

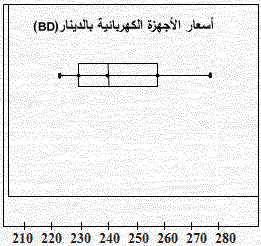
     2                        

b ) ∫ (3X ² − 4X + 5 ) dX

    0                          

السؤال الخامس:

i  يُبيّن الصندوق وطرفيه أدناه أسعار الأجهزة الكهربائية بالدينار (BD) بأحد المحلات التجارية.

   اعتمد الصندوق وطرفيه أدناه ؛ للإجابة عما يأتي :

a)  صِفّ شكل الصندوق .

b)  لخص تمركز البيانات وتشتتها باستعمال الوسط والانحراف المعياري , أو المقاييس الخمسة .

c)  أوجد المدى الرُبيعي .

الحل ( لا حظ الشكل جهة اليسار )

a)  التوزيع ذو التواء موجب

b)  المقاييس الخمسة: القيمة الصغرى i220, الرُبيع الأول i230, الوسيط i240, الرُبيع الثالث i220, القيمة العظمى i220.  

c)  المدى الرُبيعي i 260 − 230 = 30

السؤال السادس:

    في دراسة أجريت لمجموعة أشخاص حول انعقاد معرض الخريف السنوي الذي يقام في مركز

    البحرين الدولي للمعارض . تبين أنّ َi75%من المتسويقين أنهم يفضلون أن يتزامن موعد المعرض

    مع وقت استلام الراتب . إذا اختير i4أشخاص عشوائياً , وتم سؤالهم عما إذا كانوا يفضلون أن يكون موعد

    انعقاد المعرض مع وقت استلام الراتب , وكان المتغير العشوائي X يدل على عدد الأشخاص الذين أجابوا

     بنعم . اعتمد جدول التوزيع ذا الحدين أدناه ؛ للإجابة عما يأتي:

   a) مثل جدول التوزيع ذا الحدين بالأعمدة .     

   b) أوجد احتمال أن ثلاثة منهم على الأقل أجابوا عن السؤال بنعم . 

   c) أوجد الوسط والتباين لها التوزيع , ثم فسر معانيها في سياق الموقف .

   الحل

n = 4 , p = 0.75 , q = 1 − 0.75 = 0.25 ,  X = 1 , 2 , 3 , 4 المتغير العشوائي

    b) احتمال أن ثلاثة منهم على الأقل يعني احتمال ثلاثة أو أربع أي:

 P(X ≥ 3) = P(3) + P(4) = 0.42 + 0.32 = 0.74

    c) الوسط : μ = n p = 4 × 0.75 = 3

        التباين : σ² = n p q = 4 × 0.75 × 0.25 = 0.75

        التفسير: الوسط i3 يعني ثلاثة أشخاص من أربعة أجابوا بنعم أي يفضلون انعقاد المؤتمر مع صرف الرواتب.

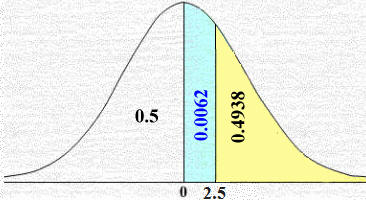
السؤال السابع:

         قامتإحدى المؤسسات الخيرية بإجراء دراسة ميدانية تتعلق بمقدار ما ينفقه أرباب الأسر في بداية كل شهر

         على المستلزمات المنزلية . إذا كانت البيانات موزعة توزيعاً طبيعياً بوسط μ = BD 190 , وانحراف

          معياري σ = BD 12 . فأوجد الاحتمالات المطلوبة , وارسـم المساحة تحت المنحنى والمرتبطة بالاحتمال .

( تنبيه : مرفق جدول التوزيع الطبيعي المعياري بصفحة i9)

   a)ا( P ( X ≥ 220  .

   b)ا( P ( 175 < X < 226  .

الحل

a) P (X ≥ 220 )

  X − μ        220 −190        30

    Z = ———— = ————— = —— = 2.5

     σ                   12             12  

     من جدول Z ومن العمود الأول مقابل i2.5نجد القيمة i0.4938فتكون المساحة تحت المنحنى:

المساحةi= 0.5 − 0.4938 = 0.0062

b) P (175 < X < 226 )

X − μ        175 −190     −15   

     Z = ———— = ———— = —— = −1.25

      σ                 12           12     

   X − μ         226 − 190        36

   Z = ———— = ————— = —— = 3

        σ                  12              12

     من جدول Z ومن العمود الأول مقابل i−1.25نجد القيمة i0.3944

     من جدول Z ومن العمود الأول مقابل i3.0نجد القيمة i0.4987

     والمساحة تحت المنحنى المطلوبة بجمع قيم Z الجدولية : i 0.3944 + 0.4987 = 0.8931

( أنتهت الأسئلة )