
ريض i261 المسار: ( توحيد المسارات ) صفحة (i1) لاحظ أن أسئلة الامتحان في i6صفحات
مملكة البحرين
وزارة التربية والتعليم
إدارة الامتحانات / قسم الامتحانات
امتحان نهاية الفصل الدراسي الأول للتعليم الثانوي للعام الدراسي i2012/2011
اسم المقرر: الرياضيات i3 المسار: توحيد المسارات
رمز المقرر: ريض i261 الزمـــن: ساعة ونصف
=================================================================================================================
أجب عن جميع الأسئلة الآتية
ملاحظة: جميع الأشكال الواردة في الامتحان تقريبية
السؤال الأول:
ضع دائرة حول ومز الإجابة الصحيحة في كل مما يأتي:
( i1) إذا كان هناك i4خطوط باص من المدينة A إلى المدينة B و i3خطوط باص من المدينة B إلى المدينة C
بكم طريقة يستطيع أحد الركاب أن ينتقل من المدينة A إلى المدينة C ماراً بالمدينة B ? الحـل
عدد الطرقi= 4 × 3 = 12 │ A 14 B 12 C 8 D 7
( i2) بكم طريقة يمكن أن يجلس i6أشخاص في شكل حلقة ؟ الحـل
عدد الطرقi= ( n - 1 )! = ( 6 - 1 )! = 5! │ A 8! B 7! C 6! D 5!
( i3) ما احتمال ظهور العدد i2عند رمي مكعب مرقم من1iإلى i6مرة واحدة , إذا علم أن
العدد الظاهر على الوجه العلوي هو عدد زوجي ؟ الحـل
الاحتمالi= P(B/A) = P(A∩B)/P(A) = (1/6) / (3/6) = 1/3 │ A 1/3 B 1/6 C 1/2 D 2/3
( i3) لدى مريم i9أحرف بلاستيكية ي , ح , ب , ر , ي, ل , ن , أ . إذا اختارت تبديل واحد من هذه الحروف
(من سبعة أحرف) لتكوين كلمة عشوائياً , فما احتمال أن تكون الكلمة هي "البحرين" ؟
2! 9! 1 1
A —— B —— C —— D ——
9! 2!2! 9! 2!9!
( i4) حذف

A X = − 3 B X = 0 C X = 1 D X = 3 الحـل
X − 3 = 0 (المقام ≠i0) à X = 3 │
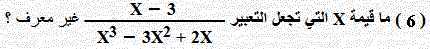
A 0 , − 1 , − 2 B − 1 , − 2 C 0 , 1 , 2 D 1 , 2 الحـل
X3 − 3X2 + 2X = 0 (المقام ≠i0)
X( X2 − 3X + 2) = 0 à X(X − 1)(X − 2) = 0 à X = 0 , X = 1 , X = 2 │
================================================================================================================
السؤال الثاني: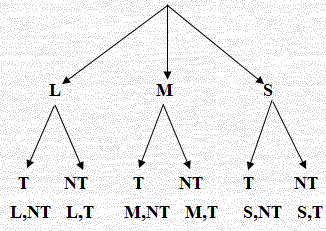 الحل
الحل
( i1) يبيع محل تجاري الآيس كريم في أكواب ذات حجم صغير (S) , أو حجم متوسط (M) , أو حجم كبير (L) , ومع صلصة (T)
، أو دون صلصة (NT). مثل فضاء العينة لتراتيب أنواع الآيس كريم باستعمال طريقة الشجرة البيانية. ===============================================================================
( i2) إذا كانت فرصة منى للفوز في مسابقة رياضية i0.6, فما هو احتمال عدم فوزها في المسابقة ؟
الحل :
بفرض A حدث فوز منى فإنَّ: حدث عدم الفوز هو Ᾱ
P( A ) = 0.6 à P( Ᾱ ) = 1 − P( A ) = 1 − 0.6 = 0.4
===============================================================================
( i3) إذا طُّلب إليك ترتيب المضلعات أدناه في صف من اليمين إلى اليسار, فما هو احتمال أن يكون المستطيل هو الأول والمثلث هو الثاني ؟

الحل :
عدد الترتيبات هو i!4 ومع ثبات المستطيل والمثلث في أول الصف فيكون تركيب الشكلين الآخرين هو i!2وبفرض A الاحتمال المطلوب فإنَّ:
P(A) = 2! / 4! = 2×1 / 4×3×2×1 = 1 / 12
========================================================================================
السؤال الثالث:
( i1) يرغب مشرف الإذاعة المدرسية في تشكيل لجنة إذاعية مكونة من i4طلاب يتم اختيارهم من i10طلاب عشوائياً.

( i2) يسدد أحمد بندقيته نحو الهدف كما في الشكل أدناه , ما احتمال أن يصيب المنطقة المظللة ؟

( i3) حدد إذا كان الحدثان الآتيان مستقلين أو غير مستقلين:
a) سحبت كرة من صندوق به i10كرات حمراء , ثم أعيدت إليه وسحبت كرة ثانية. حدثان مستقلان
b) إذا كان المعدل التراكمي لإبراهيم في شهادة الثانوية العامة i95% فما فوق , فسيحصل على بعثة دراسية. حدثان غير مستقلين
( i4) صندوق به i25بطاقة مرقمة من i1إلى i25, سحبت منه بطاقة واحدة عشوائياً , ما احتمال أن تحمل
البطاقة المسحوبة عدداً زوجياً أو أكبر من i15؟
الحل :
بفرض A حدث العدد زوجي , B حدث العدد أكبر من i15و A ∩ B حدث العدد زوجي وأكبر من i15و AUB الحدث المطلوب فإنَّ:
P(AUB) = P(A) + P(B) − P(A∩B) àP(AUB) = 12/25 + 10/25 − 5/25 = 17/25
==========================================================================================
السؤال الرابع:
( i1) إذا كانت Y تتغير طردياً مع x , وعكسياً مع z , وكانت x = 12 عندما z = 1 , y = 3 فأوجد قيمة x عندما y = 9 , z = −1
الحل :
y1z1 : x1 = y2z2 : x2 à 3 × 1 : 12 = 9 × −1 : x à 1 : 4 = −9:x à x = −36
( i2) بسط كل مما يأتي:
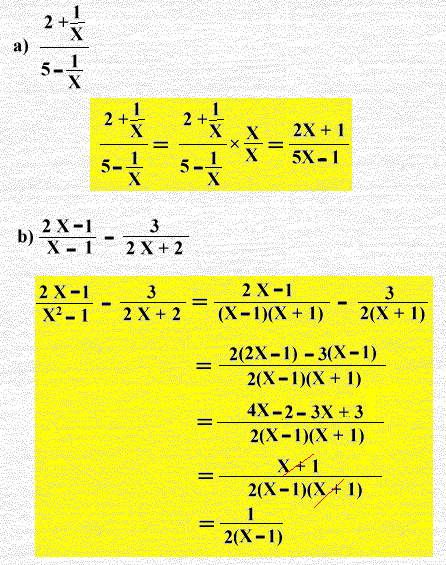
================================================================================
السؤال الخامس:
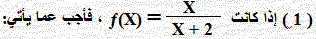
a) أكمل الجدول الآتي:
|
X |
−4 |
−3 |
−2 |
−1 |
0 |
1 |
2 |
|
ƒ(X) |
2 |
3 |
غير معرفه |
−1 |
0.5 |
≈ 0.33 |
0.5 |
بالتعويض عن قيم X في الدالة ونسجل النواتج في الجدول
b) استعن بالجدول لتمثيل الدالة بيانياً.

c) ما هو صفر الدالة ؟
قيمة X التي تجعل البسط = صفر أي: X = 0
d) حدد خطوط التقارب الأفقية والرأسية.
خط تقارب أفقي عند y = 1 وخط تقارب رأسي عند X = −2
( i2) أكمل الفراغات الآتية لتحصل على عبارة رياضية صحيحة.

............... إلى اليمين , وإزاحة i3وحدات إلى ............ , وانعكاس حول المحور ............ ( الإجابة: وحدة واحدة , الأسفل , X على الترتيب)
( i3) يحتاج عادل وخالد إلى i28ساعة عمل لبناء سور معاً , بينما يحتاج خالد إلى i34ساعة عمل إذا قام
ببناء السور وحده , كم ساعة عمل يحتاج عادل إذا قام ببناء السور وحده ؟
بفرض X عدد الساعات التي يحتاجها عادل لإنجاز العمل فيكون معدل عمل عادل هو i 1/Xمن العمل في الساعة
1/34 + 1/X = 1/28 à 1/X = 1/28 - 1/34 = 3/476 à X = 476/3 = 158⅔
=======================================================================================================