امتحان الأردن للثانوية العامة (الورقة الأولى) للعام 2003م الدورة الشتوية

يفضل استخدام الخط المتوسط من View, Text size, medium  لاحظ الصورة في اليسار

السؤال الأول :    

يتكون هذا السؤال من (7) فقرات من نوع الاختيار من متعدد ، يلي كل فقرة أربع إجابات ،

واحدة منها فقط صحيحة :

                   س² – س

1)  نهـــــــــــــا ــــــــــــــــــــــــ  تسـاوي

     س ←1     س²– 1

                                                                1

    أ) 1                     ب)2                     جـ)  ـــــ                         د) صفر

                                                                2

                                                                                                     س

2) إذا كانت نهـــــــــــــا ق(س) = 7   فما قيمة : نهـــــــــــــا(ق(3س – 1) + [ ــــــ + 5] ) ؟

                 س ←2                                   س ←1                           3

   أ) 12                   ب) 27                  جـ) 27                         د) غير موجودة 

3) إذا كان متوسط تغير الاقتران ق(س) في الفترة  [ –4 ، 1 ]  يساوي (3) وكان ق(1) = 2 ،

     فما قيمة ق(–4) ؟

   أ) 11                   ب) – 13                  جـ) – 11                        د) 13

4) إذا كان ق(س) × هـ (س)  = 1 وكان هـ(1) = 3 ، هـ^/(1) = 5 فما قيمة ق^/(1) ؟

      4                             5                         5                                 5

   أ) ـــ                     ب) – ـــ                    جـ) ــــ                             د) ـــ

      9                             9                         9                                 3

5) إذا كان ق(س) = س²( | س | )⁵ ، وكان هـ^/(2) = 4 ، هـ(2) = – 1 ،  فما قيمة ( ق o هـ )^/(2) ؟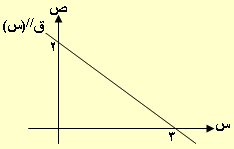

    أ) – 18                  ب) 28                    حـ) 7                              د) – 10

6) يمثل الرسم المجاور منحنى ق^//(س) للاقتران ق(س) فما إحداثيات نقطة انعطاف منحنى ق(س)؟

    أ) (3 ، 0)               ب) (0 ، 2)              حـ) (3 ، ق(3) )                د) (0 ، ق(0) )

                                                  p                                                                                                                          p  

7) إذا كان ق(س) = حا2س ، س ' [ ـــــ ، p] ، فجد قيمة س₁التي تحصل عليها من تطبيق نظرية رول على الاقتران ق(س) في الفترة [ ـــــ ، p ]

                                                  2                                                                                                                           2   

        p                          p                                                    ــ        3 p

    أ) ـــــ                    ب) ـــــ                     حـ) p                             د) ــــــــ      

        2                          4                                                               4

السؤال الثاني :    

                              حا²س

   أ) أوجد   نهـــــــــــــا ــــــــــــــــــــ 

                س ←0    قاس – 1

السؤال الثالث :    

                                                                  3  ــــــ                   

أ) باستخدام نظرية بلزانو أوجد التقريب الثاني للعدد  /\ 9   لأقرب منزلة عشرية واحدة

ب) استخدم تعريف المشتقة الأولى لإيجاد ق^/(س) للاقتران :

                    ــــــــــــــــــ

    ق(س) = /\2 س + 1   حيث س > –  ¹

                                                     2    

ج) ارسم منحنى تقريبياً للاقتران ص = ق(س) ، إذا علمت أن :

     ق(2) = صفر ،  ق^//(س) < صفر عندما س < 2 ، ق^//(س) > صفر عندما س > 2 ، ق^/(س) < صفر لكل س ' ح

السؤال الرابع :    

أ) أوجد معادلة كل من المماس والعمودي على المماس لمنحنى العلاقة :

     س²– ص² = 16  عند النقطة (5 ، –3)

ب) إذا كان ص = جاس + جتاس ، أثبت أن :

            د² ص

      ص ـــــــــــــ + 1 = – حا2 س

            د س² 

ج)  يتحرك جسيم في خط مستقيم فيقطع مسافة ف متراً في زمن ن ثانية حيث :

      ف = ن³ ـ 7ن² + 9ن + 1

     أوجد تسارع الجسيم عندما تكون سرعته 1م/ث .  

السؤال الخامس : 

                          4 س                                        د ص            

    أ) إذا كان ل = ــــــــــــــــــ     ،  ص = ل²     ،  فجد  ـــــــــــ

                       2 س + 1                                     د س

    ب) إذا كان ق(س) = | س – 2 | + | س | ، فبين أن ق^/(0) غير موجودة

                                          س⁴

    ج) إذا كان ق(س) = س³ – ــــــــ   ،  س ' [ –1 ، 4 ] أوجد ما يلي :

                                          4   

      1)   فترات التزايد وفترات التناقص للاقتران ق(س) .

      2)    القيم العظمى المحلية والقيم الصغرى المحلية للاقتران ق(س) وبين المطلقة منهما .

      3)   فترات التقعر للأعلى وفترات التقعر للأسفل لمنحنى الاقتران ق(س) .

السؤال السادس :

أ) يقف رجل على رصيف حول للسفن ، ويسحب حبلاً أحد طرفيه متصلاً بقارب وطرفه الآخر يمر ببكرة ترتفع (1.2) متراً عن خط سير القارب ،

                                                                                         3

   فإذا كانت سرعة تزايد الزاوية بين خط سير القارب والحبل تساوي  ــــــ  راديان/ ثانية عندما كان القارب على بعد (1.6) متراً عن الرصيف ،

                                                                                        20

   فما السرعة التي يسحب بها الرجل الحبل ؟

                                                                                                                                                                      س²

ب) أ ب جـ د مستطيل يقع رأساه  ب ، جـ على محور السينات ،  ويقع الرأس أ في الربع الأول على منحنى الاقتران  ق(س) = 12 – ـــــــ  ،

                                                                                                                                                                         4

      ويقع د في الربع الثاني على منحنى الاقتران هـ (س) = 12–  س² ، أوجد أكبر مساحة ممكنة للمستطيل أ ب جـ د .