السؤال الأول :    

                             1 – حتا 6س      – 9

أ) أثبت أن نهـــــــــــــا ــــــــــــــــــــــــ =  ـــــــ

               س ←0   حتا 8 س –1      16 

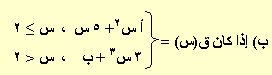
   قابلاً للاشتقاق عند س = 2 , أوجد قيمة كل من أ , ب .

                                                              1

  ج) أوجد معادلة المستقيم الذي يمر بالنقطة ( 2 ، ــ ) ويكون عمودياً على المنحنى ص = س² .

                                                                2

السؤال الثاني : 

   أ) برهن صحة النظرية الآتية :
     إذا كان ق(س) = س ^ن , حيث ن عدد صحيح موجب ، فإن ق^/ (س) = ن س ^ن–1

                                 س – 1

  ب) إذا كان ق(س) =  ــــــــــــــــــ

                             س² + 3

    أوجد : 1. فترات التزايد للاقتران ق(س) .

             2. فترات التناقص للاقتران ق(س) .

  ج) صفيحة معدنية مستطيلة الشكل تتمدد بانتظام بحيث يبقى طولها يساوي ثلاثة أمثال عرضها . أوجد معدل التغير في مساحة هذه الصفيحة بالنسبة

      إلى طولها عندما يكون طولها 15 سم .

السؤال الثالث : 

يتألف هذا السؤال من (6)  فقرات من نوع الاختيار من متعدد , يلي كل فقرة أربع إجابات واحدة منها فقط صحيحة ، والمطلوب أن تكتب في دفترك رقم الفقرة وبجانبه رمز الإجابة الصحيحة لها .

                        1                4

1)  نهـــــــــــــا ( ــــــــــــــــ  –  ـــــــــــــــــ )  تساوي :

       س ←2      س – 2        س²– 4

           1                     1

      أ)  ــــ               ب)  ـــ                  ج) صفر                 د) غير موجودة  

          2                     4

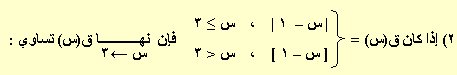
      أ) 2            ب) 3               ج) 1                    د) غير موجودة

3)  إذا كان ق(س) = س³ + 2س ,   هـ (س) = س²     فإن  ( ق^/ o هـ )^/ (1)   تساوي :  

      أ) 12           ب) 6            ج) 10               د) 16

4) من الشكل المجاور والذي يمثل منحنى ق(س) المعرف على الفترة [ 1 , 4] ، فإن النقطة (3 , ق(3)) هي نقطة :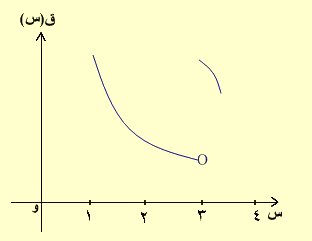

       أ)  انعطاف .    

    
       ب)  قيمة عظمى مطلقة .      

       ج)  قيمة صغرى مطلقة .     

        د)  قيمة عظمى محلية .

5) إذا كان ق(س) = | 3 – س | فإن (ق²)^/(1) تساوي :

        أ) 4            ب) ـ4                  ج) 1            د) غير موجودة

6) إذا علمت أن ق(س) = [ 2 س – 1 ] حيث س ' [ 0 ، 1 ] فإن مجموعة قيم س الحرجة هي :

                                                                                                       1

    أ) { 0 ، 1 }             ب) ( 0 ، 1 )            ج) [ 0 ، 1 ]            د) { 0 ، ــــ ، 1 }

                                                                                                       2

السؤال الرابع : 

   ب) يتحرك جسيم في خط مستقيم طبقاً للمعادلة :

    ف(ن)=ن³–3ن²+ 3ن+3, حيث ف(ن) المسافة بالأمتار، ن الزمن بالثواني أثبت أن الجسيم يتوقف مرة واحدة دون أن يغير من اتجاه حركته

                             ــــــ 

   ج) إذا كان ق(س) = /\س ، وكان المماس عند س=4 موازياً للوتر الواصل بين النقطتين (1، ق(1))، (م، ق(م))، حيث م>1. جد قيمة م

السؤال الخامس :

                                                                         –2     2            

    أ) إذا كان الاقتران ق(س) = 9 س³ – 4 س ,  س ' [ ــــــ  ،  ــــ ]

                                                                            3      3

    1) بين أن ق(س) يحقق شروط نظرية رول على الفترة المعطاة .

  2) جد قيمة س₁ التي تعنيها نظرية رول على الفترة المعطاة .

  ب) إذا كان ص = ظا(س ص ) ، أثبت أن :

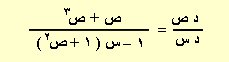
                                    1                             –3

   ج) إذا كان ق(س) = ــــــــــــــــــــ    ،  حيث س ≠ ــــــ  ،  وكانت ق^/ (1) = 2 أوجد قيم الثابت أ .

                               3 + أ س                          أ

السؤال السادس :

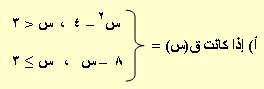
    أوجد : 1) القيم العظمى والصغرى المحلية للاقتران ق(س) .

           2) فترات التقعر للأعلى وللأسفل ( إن وجدت )

 ب) إذا كان ق(س) = س³ + س + 1 معرفاً على ح . باستخدام نظرية بلزانو والمشتقة ، أثبت أنه يوجد صفر واحد للاقتران ق(س)

      في الفترة ( ـ1 , 0) ، ثم أوجد التقريب الثاني لهذا الصفر .

ج) ارسم منحنى تقريبياً للاقتران ص = ق(س) إذا علمت أن :

    ق(1) = 1 ،  ق^/ (س) > صفر لكل س ' ح ،  ق^// (س) > صفر  عندما س > 1  ،  ق^// (س) < صفر عندما س < 1

السؤال السابع :

    أ) أ ب جـ مثلث طول قاعدته ب جـ يساوي 12 سم , وطول ارتفاعه النازل من الرأس أ يساوي 16 سم , فرضت نقطة د على ب جـ ثم رسم مستقيم

        يوازي ب جـ ويقطع أب , أجـ في النقطتين هـ , و . احسب طول العمود النازل من د على هـ و لتكون مساحة المثلث هـ د و أكبر ما يمكن .

   ب) دائرتان متحدتان في المركز ، نصفا قطريهما 3 سم , 18 سم . ابتدأت الدائرة الصغرى تتسع بحيث يزداد نصف قطرها بمعدل 2سم / د.

        وفي نفس اللحظة أخذت الدائرة الكبرى تصغر بحيث يتناقص نصف قطرها بمعدل 3 سم / د . أوجد معدل التغير في المساحة المحصورة بين

        الدائرتين في اللحظة التي تصبح هذه المساحة تساوي صفراً .