السؤال الأول :    

   أ) إذا كان ق(س) = س³ – 3س + 1 ، باستخدام نظرية بلزانو :

        1- أثبت أنه يوجد صفرين موجبين للاقتران .

        2- جد قيمة تقريبية لكل منهما لأقرب منزلة عشرية واحدة .

                        2 – س      

ب) جد نهـــــــــــــا ــــــــــــــــ

         س ← 2   حاp س  

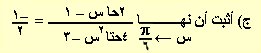
السؤال الثاني : 

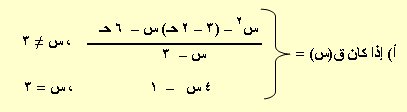
     متصلاً عند س = 3 ، فما قيمة جـ .

 ب) باستخدام تعريف المشتقة ، ابحث قابلية الاقتران ق(س) = 2 + |2 –  س |

     للاشتقاق عند س = 2

 ج) برهن أنه إذا كان الاقتران ق(س) قابلاً للاشتقاق عند س = أ ، فإنه يكون متصلاً عند س = أ .

 السؤال الثالث :

يتألف هذا السؤال من (5) فقرات من نوع الاختيار من متعدد ، يلي كل فقرة أربع إجابات واحدة منها فقط صحيحة .

                                           س

 2) إذا كان ق(س) = س [ 2 –  ـــــ ] ،  فإن ق^/ (3) تساوي :

                                           3

     أ) صفر              ب) 1                    ج) 2                     د) غير موجودة

 3) إذا كان ( ق o هـ)^/ (3) = 15 ،  حيث ق(س) = س²– 9 ،  هـ^/ (3) = 5 فإن هـ(3) تساوي :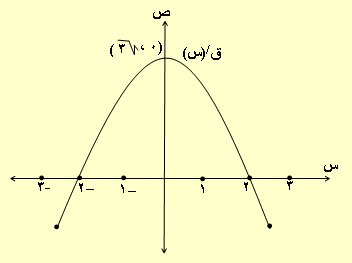

     أ) صفر              ب) 1.5                   ج) 3                     د) 6

 4) الشكل المجاور يمثل منحنى المشتقة الأولى للاقتران ق(س) ،

     المعرف على [ـ3 ، 3] فإن زاوية الانعطاف هي :    

     أ) صفر ^ه             ب) 30^ه                   ج) 60^ه                  د) 90^ه

      أ) {0 ، 16}            ب) {0 ، 8 ، 16}               ج) {8}                د) غير موجودة

 السؤال الرابع :

   أ) إذا كان متوسط تغير الاقتران ق(س) على الفترة [–1 ، 3] يساوي 4 ، فجد متوسط تغير الاقتران هـ (س)=2ق(س)+3س على الفترة نفسها.

                                                                       د ص

    ج) إذا كان س = ق(ص² + 1) ،  ق^/ (5) = 4 ، جد ــــــــــ  عند ص = 5

                                                                       د س
 

السؤال الخامس :

أ) قذف جسيم رأسياً إلى الأعلى بحيث أن ارتفاعه من نقطة القذف بالأمتار بعد  ن  ثانية يعطى وفقاً للاقتران  ف(ن) = ع₁ ن – 5 ن² .

   فإذا علمت أن أقصى ارتفاع وصل إليه الجسيم هو 20م ، فما قيمة ع₁.

ب) من النقطة م (1 ، 2) ، رسم مماسان لمنحنى الاقتران  ص = 2س – س² ، فمسّاه في النقطتين ك ، هـ ، جد مساحة المثلث م ك هـ .

                               ك(س)

  ج) إذا كان ق(س) = ـــــــــــــــ ، هـ(س) ≠ صفر ، وكان طلاً من ك(س) ، هـ(س) قابلاً للاشتقاق عند س = أ ، ق^/ (س) = صفر ،

                              هـ(س) 

                                    ك^/ ( أ )

       أثبت أن :   ق( أ ) = ــــــــــــــــ

                                   هـ^/ ( أ )

السؤال السادس :

                                                                                                p                

    أ) بتطبيق نظرية رول على الاقتران ق(س) = س جتا س ، س '  [ 0 ، ـــــــ ]   أثبت أنه يوجد حل واحد على الأقل للمعادلة طتا س = س .

                                                                                                2

ب) إذا كان ق(س) = س³ + س² – 5س + 1 ،  س ' [ – 2 ، 2 ] جد

    1) فترات التزايد والتناقص للاقتران ق(س) .

    2) نقط القيم القصوى المحلية ونوعها .

ج) ارسم منحنى تقريبياً للاقتران ص = ق(س) إذا علمت أن :

     ق(0) = 1 ، ق(2) = 3 ، ق^/ (0) = ق^/ (2) = 0

     ق^/ (س) < 0 عندما | س – 1 | > 1 ،  ق^/ (س) > 0 عندما | س – 1 | < 1

     ق^// (س) > 0 عندما س < 1 ،  ق^// (س) < 0 عندما س > 1

السؤال السابع :

أ) كرة مصمته نصف قطرها 10سم ، حُفر بداخلها متوازي مستطيلات قاعدته مربعة الشكل ، وارتفاعه ع سم .

                                                                                                        1

      1- أثبت أن حجم متوازي المستطيلات يعطي بالعلاقة الآتية : ح = 200 ع + ـــ ع³ 

                                                                                                          2

      2- جد أبعاد متوازي المستطيلات لتعطي أكبر حجم ممكن له .

 ب) خزان على شكل مخروط دائري قائم رأسه إلى أسفل ، ارتفاعه 24دسم ، نصف قطر قاعدته 8دسم ينساب الماء من فتحة في رأسه إلى إناء

      اسطواني الشكل موجود أسفله وقطر قاعدته 12د سم . جد معدل ارتفاع الماء في الإناء الاسطواني عندما يكون ارتفاع الماء في الخزان

      المخروطي 12دسم ، ومعدل انخفاض الماء في الخزان المخروطي 1دسم / دقيقة .