السؤال الأول :    

                              حا2س – حا2 أ     

 أ) أثبت أن نهـــــــــــــا ــــــــــــــــــــــــــــ = 2 حتا2 أ  ،  س ≠ أ

                س ← أ       س – أ    

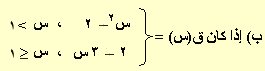
  وكان هـ(س) = 15 – 3 ق(س) ، ابحث في اتصال هـ(س) عند س = 1

السؤال الثاني : 

     أ- إذا كان س + ص = س ص ، أثبت أن :

                      2 ص²

         ص^// =  ـــــــــــــــ

                       س²

    ب- إذا كان منحنى ق(س) = أ س² + ب س + جـ  يقطع محور الصادات في النقطة (0 ،3) ، وله مماسان ، المماس الأول عند النقطة س = –1    ويصنع زاوية مقدار 45^ه مع الاتجاه الموجب لمحور السينات ، والمماس الثاني عند النقطة س = 2 ويصنع زاوية مقدارها 135^ه مع     الاتجاه الموجب لمحور السينات . جد القيم أ ، ب ، جـ .

                د ص

    ج-  جد  ــــــــــ  لما يلي :

                د س

    2) 2 ص = ق(2س² – س) ،  ق^/ (6) = 4 عند س = 2

    3)  س + ظا (س ص) = صفر

السؤال الثالث : 

   ج- يتحرك جسم في خط مستقيم وفق المعادلة الزمنية الآتية : ف(ن) = 6ن²–  ــــ ن³ ، حيث ف المسافة المقطوعة بالأقدام بعد ن ثانية.

                                                                                                        1 

                                                                                                          3

       جد ما يلي :

        1- سرعة الجسم عندما ن = 5 ثواني .

        2- تسارع الجسم عندما تنعدم سرعته.

السؤال الرابع :

أ- باستخدام تعريف المشتقة الأولى ، جد ق^/ (س) للاقتران :
 

                        س

      ق(س) = ــــــــــــــــ  ،  س ≠ 2

                    س – 2

ب- إذا كان ق(س) = س – 1 ، هـ (س) = –2 س + 2 اقترانيين معرفين على الفترة [–1 ،2] ، باستخدام نظرية بلزانو :

    1- أثبت أنه يوجد جـ ' (– 1 ، 2 )  بحيث أن : ق(جـ) = هـ(جـ) .
 

    2- جد قيمة جـ .

                                 3

                                 ـــ

ج- ليكن ق(س) = ( س)⁵  

      جد ما يلي :

      1- مجالات التزايد والتناقص للاقتران ق(س) إن وجدت .

      2- مجالات التقعر للأعلى وللأسفل للاقتران ق(س) إن وجدت .

      3- ارسم منحنى تقريبياً للاقتران ق(س) .

السؤال الخامس :

    يتألف هذا السؤال من (6) فقرات من نوع الاختيار من متعدد ، يلي كل فقرة أربع إجابات واحدة منها فقط صحيحة ، والمطلوب أن تكتب في دفترك رقم الفقرة وبجانبه رمز الإجابة الصحيحة لها .

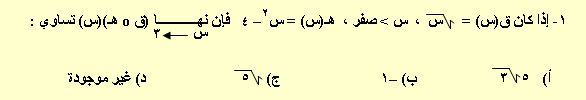
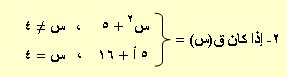
        فإن قيمة أ التي تجعل ق(س) متصلاً عند س = 4 هي :

                                                25                             37

         أ) – 1                         ب)  ــــــ                        ج) ــــــ                        د) 1

                                                16                              5

                                                                ق( –3 + هـ) –  ق(–3)

     3- إذا كان ق^/ (–3) = 3  فإن نهــــــــــــــــا  ــــــــــــــــــــــــــــــــــــــــــــــ  تساوي :

                                               هـ ← 0                   –3 هـ

         أ) 3                            ب) –3                         ج) –1                        د) 1

     4- إذا كان ق^/ (س) اقتراناً معرفاً على الفترة ( – 2 ، 3 ) ، وكان ق^/ (1) = صفر ،  ق^// (1) = – 7 ،  ق(1) = – 5 ،

          فإن مقدار القيمة العظمى المحلية للاقتران ق هي :

        أ) – 5                         ب) – 7                         ج) 1                         د) صفر

                                                                                             (–1)^ن  ن!

     5- إذا كانت المشتقة النونية للاقتران ق(س) تساوي  ق^(ن)(س) = ـــــــــــــــــــــــــــــــــــ  فإن ق⁽⁵⁾(س) للاقتران ق(س) هي:

                                                                                                س ^ن+1

             24                            – 120                         – 720

        أ)  ــــــــ                      ب) ـــــــــــــ                    ج) ــــــــــــــ                  د) غير ذلك                              

            س⁵                              س⁶                              س⁷

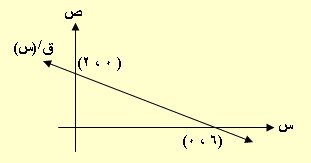
     6- من الشكل المجاور  ،   ق^/ (س)

        تساوي :

                                        1                                              – 1

        أ) – 3                  ب) ـــــ                ج) 3                   د) ــــــ   

                                        3                                               3

السؤال السادس :

    أ- مثلث متساوي الساقين طول قاعدته ثابت ويساوي ل ، إذا كان طول كل من ساقيه يتناقص بمعدل 3سم / دقيقة .

     جد معدل تناقص مساحة المثلث عند اللحظة التي يكون فيها طول كل من الساقين مساوياً لطول القاعدة .

 ب- أ ب جـ د مستطيل يقع داخل المنحنيين : ق(س) = 2 س² ، هـ(س) = 36 – س² ، بحيث أن رأسيه أ ، ب يقعان على المنحنى ق(س) ،

      ورأسيه جـ ، د يقعان على المنحنى هـ (س) . جد بعدي المستطيل أ ب جـ د والتي يمكن رسمهما لتكون مساحته أكبر ما يمكن .

 ج- أثبت أن المستقيم 2ص + س = 3 عمودي على المنحنى ص = س² ، عند إحدى نقطتي تقاطعه مع المنحنى دون الأخرى .