(1) أوجد الجذرين التربيعيين للمقدار – 8ت                                                                            [الجواب ± (2 – 2ت)]

 

                                                31 + 17ت

(2) أوجد الجذرين التربيعيين للمقدار ــــــــــــــــــــــــ                                                                  [الجواب ± (4 + 4ت)]

                                                   1 – ت 

                    ــــــــــــــــــــــــــ          

                     13(1 – 5ت)

(3) إذا كان  /\ــــــــــــــــــــــــــــ  = س + ص ت فما قيمة كل من س ، ص الحقيقية                           [الجواب ± 3 ، –(± 2)]

                        5 – ت   

 

 

(4) إذا كانت (س + ص ت)2 = 8 – 6ت فأوجد جبرياً القيم الحقيقية لكل من س ‘ ص وحقق الناتج بيانياً    [الجواب ± 3 ، –(± 1)]

 

 

 

(5) أوجد الجذر التربيعي للمقدار 21 + 20 ت وإذا كانت س =21 + 20ت فأوجد قيمة س0.5+ 29س–0.5 [الجواب ± (5 +2ت)، ± 10]

 

                        

                         36 – 2 ت

(6) ضع المقدار  ــــــــــــــــــــــــــ  في الصورة  س + ص ت                                                          [الجواب8 – 6ت،±(3 – ت)]

                          3 + 2 ت   

 

      ثم أوجد بيانياً الجذر التربيعي للناتج وحقق ذلك جبرياً.    ( الإرشاد أسفل الصفحة)

 

 

(7) أوجد الجذر التربيعي للكية المركبة – 8 – 6ت                                                                     [الجواب ±(1 – 3 ت)]      

 

 

(8) أوجد الجذر التربيعي للكية المركبة 15 – 8ت ومثل العدد المركب وجذريه بيانياً                            [الجواب ±(4 – ت)]

     

 

 

(9) إذا كان ع1= 1+ ت ، ع2= 1– ت فأوجد قيمة:  (ع1)2 +  ع1ع2 +  (ع2)2

 

                                                                                                                                                  ــــ 

      ثم استخدم ذلك في إيجاد الجذر التربيعي للمقدار (ع1)3 – (ع2)3                                               [2 ، ±/\2 ( 1 + ت)]

 

                      ــــــــــــــــــــــــــ          

                       11 – 2 ت

(10) إذا كان  /\ــــــــــــــــــــــــــــ  = س + ص ت فما قيمة كل من س ، ص الحقيقية                           [الجواب ± 2، ± 1]

                        1 – 2 ت   

 

     تحدد النقطة للناتج (العدد المركب) بيانياً (8 ، 6) مثلاً كما بالشكل

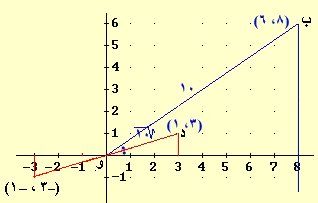
     نحسب طول الوتر (و ب) من نظرية فيثاغورث هنا = 10

     ننصف الزاوية (و) بالمستقيم و د

     نحدد طول القطعة المستقيمة على ود بطول جذر الوتر (و د) هنا جذر 10

    نهاية القطعة المستقيمة (د) تمثل الجذر الأول (3 ، 1)

    امتداد د و بقدر نفسه يمثل نهايته الجذر الآخر (– 3 ، – 1)

    نحن نتبع المقياس والسعة ل =10، هـ = و والجذر التربيعي جذر ل ونصف<هـ

    بقولنا ننصف الزاوية (و)، ويتم التحقق جبرياً كما سبق