الجذر التربيعي للعدد المركب ع = (ل ، هـ) ـ الصورة القطبية ـ
بفرض أن (ك ، ى) جذر التربيعي للعدد المركب (ل ، هـ) فإن:
(ل ، هـ) = (ك ، ى)2 نضعهم على الصورة المثلثية
ل(حتاهـ + ت حاهـ) = [ك(حتاى + ت حاى)]2 بفك القوس مع ملاحظة ت2 = –1
= ك2( حتا2ى – حا2ى + 2ت حتاى حاى ) وبمساواة الحقيقي بالحقيقي والتخيلي بالتخيلي
ل حتاهـ = ك2( حتا2ى – حا2ى ) .................. (1)
ل حاهـ = 2ك2حتاى حاى .................. (2) بتربيع (1) ، (2)
ل2حتا2هـ = ك4( حتا4ى – 2 حا2ى حتا2ى + حتا4ى ) ...... (3)
ل2 حا2هـ = 4ك4حتا2ى حا2ى ..................................... (4) بجمع (3) ، (4)
ل2( حا2هـ + حتا2هـ ) = ك4( حتا4ى + 2 حا2ى حتا2ى + حا4ى ) لاحظ: حا2هـ + حتا2هـ = 1
ل2 = ك4 (حتا2ى + حا2ى )2 = ك4 × 1 = ك4 ومنها ل = ك2 أي أن:
ــــــ
ل = /\ ك ............................... (5) نعوض في (2)
ك2حاهـ = 2ك2حتاى حاى بحذف ك2 ، حا2ى = 2حاى حتاى يكون:
حاهـ = حا2ى ومنها هـ = 2ى أي أن:
هـ
ى = ــــــ ............................... (6)
2
من (5) ، (6) نحصل على أن:
ـــــ ــــ ــــ
هـ هـ
هـ
( ك ، ى ) = ( /\ ل ، ـــــــ ) ويكون الجذران التربيعيان للعدد المركب (ل ، هـ) هما ( /\ ل ، ـــــــ ) ، ( /\ ل ، ـــــــ + π )
2 2 2
يمكن الحصول على نفس النتيجة بالتعويض في القانون السابق للجذر التربيعي
(ل ، هـ) = ل حتاهـ + ت ل حاهـ بوضع حـ = ل حتاهـ ، د = ل حاهـ فيكون
ـــــــــــــــــــــــــــــــــــــــــ ــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــ ـــــــــــــــــ
حـ + /\حـ2 + د2 – حـ + /\حـ2 + د2
س = /\ـــــــــــــــــــــــــــــــــــــ ، ص = /\ـــــــــــــــــــــــــــــــــــــ
2 2
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
ــــــــــــــــــــــــــــــــــــ ـــــــــــــــــــــــــــــــــــــ
ل حتاهـ+ /\ل2حتا2هـ + ل2حا2هـ –ل حتاهـ + /\ل2حتا2هـ + ل2حا2هـ
س = /\ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ ، ص = /\ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
2 2
ل2حتا2هـ + ل حا2هـ = ل2(حتا2هـ + حا2هـ ) = ل2 × 1 = ل2 بالتعويض في س ، ص
ــــــــــــــــــــــــــ ــــــــــــــــــــــــــــــ
ل حتاهـ + ل – ل حتاهـ + ل
س = /\ـــــــــــــــــــــــــ ، ص = /\ ـــــــــــــــــــــــــــ
2 2
ل حتاهـ + ل = ل (حتاهـ + 1) = ل [2حتا2(هـ/2) – 1 + 1] = 2ل حتا2(هـ/2)
– ل حتاهـ + ل = ل (– حتاهـ + 1) = ل [ – (1– 2حا2(هـ/2) + 1] = 2ل حا2(هـ/2) وبالتعويض في س ، ص

ــــــــــــــــــــــــــ ــــــــــــــــــــــــــ
س = /\ ل حتا2(هـ/2) ، ص = /\ ل حا2(هـ/2)
ـــ ـــ
س = /\ل حتا(هـ/2) ، ص = /\ل حا(هـ/2) ومنهم يكون
ــــ ـــ
هـ
هـ
الجذران التربيعيان للعدد المركب (ل ، هـ) هما ( /\ل ، ـــــــ ) ، ( /\ ل ، ـــــــ + π )
2 2
ط
مثال: أوجد الجذرين التربيعيين للعدد ع = ( 4 ، ــــــ ) واكتب كل منهم بالشكل الجبري ومثلهم بيانياً. تمــاريــــــــــن
3
ط ط
الحل:
الجذران هما ( 2 ، ــــــ ) ، ( 2 ، ــــــ + ط
) حيث أن ط هي π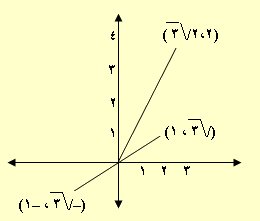
6 6
ـــــ
ط ط /\3 1
الجذر الأول جبرياً: 2 (حتا ـــــ + ت حا ــــــ ) = 2( ـــــــــ + ت ـــــ )
6 6 2 2
ــــ
= (/\3 ، 1)
ـــــ
7ط 7ط /\3 1
الجذر الثاني جبرياً: 2 (حتا ـــــــ + ت حا ـــــــ ) = 2( – ـــــــــ – ت ـــــ )
6 6 2 2
ــــ
= (–/\3 ، –1)
ـــــ
ط ط 1 /\3
العدد المركب ع جبرياً: 4(حتا ـــــــ + ت حا ـــــــ ) = 2( ــــــ + ت ــــــــ )
3 3 2 2
ــــ
= (2،2/\3 )