مقدمــة

الحاجة دفعتنا لإيجاد هذه المجموعة لعدم وجود الجذر ألتربيعي للعدد السالب (–1) مع الملاحظة بأن العدد السالب –9 هو 9 × –1 فالمشكلة

                                                                                                                                        ـــــ    

هنا بوجود الجذر للعدد السالب –1 ولذا سنعطي له رمزاً هو ت من كلمة تخيلي وأصبح لدينا الآن أن ت = /\–1، وسنرمز أيضاً للمجموعة الجديدة مجموعة الأعداد المركبة بالرمز ڪ وسنعطي الرمز ع للعدد المركب وستكون المجموعة ڪ بالصورة

ڪ = ح × ح = { ع : ع = ( س ، ص ) ، س ، ص ' ح } وسيكون س هو الجزء الحقيقي للعدد المركب، ص جزءه التخيلي أي بالإمكان كتابة العدد المركب بصورة عامة بالشكل ع = س+ ص ت مثل 3 + 2ت ، 5 – ت ، ت ، ... وبالطبع يمكن تمثيل المجموعة كما هو الحال مع ح بأن يكون المحور السيني ممثلاً للجزء الحقيقي والمحور الصادي ممثلاً للجزء التخيلي وهذا يقودنا إلى القول الآتي:

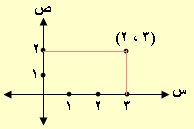
ع = 3 + 2ت أو ع = (3 ، 2) أو ع = س + ص ت والشكل الهندسي كما مبين يمثل العدد ع المركب

تعرف الصورة ع = س + ص ت بالصورة الجبرية للعدد المركب

تعرف الصورة ع = ( س ، ص ) بالصورة الهندسية للعدد المركب أو الديكارتية

وتجرى العديد من العلاقات والعمليات على ڪ

إذا كانت ع₁ = ( س₁ ، ص₁) ، ع₂ = ( س₂ ، ص₂) فإن:ـ

ع₁ = ع₂  يؤدي إلى  س₁ = س₂ ، ص₁ = ص₂  " تساوي عددان مركبان يعني تساوي الجزأين الحقيقيين وتساوي الجزأين التخيليين "

ع₁ = 0 يعني س = 0 ، ص = 0

ك ع₁ = ( ك س₁ ، ك ص₁ ) ' ڪ

ع₁ + ع₂ = ( س₁ + س₂ ، ص₁ + ص₂ ) ' ڪ   " ( ڪ ، + ) زمرة إبدالية محايدها (0 ، 0) ، –ع النظير الجمعي للعدد ع "

لكل ع₁ ، ع₂' ڪ^*: ع₁× ع₂ = ( س₁س₂ – ص₁ص₂ ، س₁ص₂ + س₂ص₁ ) ' ڪ^*  " ت² = –1 ، ڪ^* = ڪ – {(1 ، 0)}

حيث ت²= ت × ت = (0 ، 1) × (0 ، 1) = ( 0 × 0 – 1 × 1 ، 0 × 1 + 1 × 0 ) = (–1 ، 0 ) = –1

  ت³ = ت² × ت = –1 × ت = – ت  ، ت⁴ = ت² × ت² = –1 × –1 = 1 وعليه يكون:

  ت^ك = ت^م حيث م باقي قسمة ك على 4 مثل ت³³ = ت¹ = ت ،  ت²⁷ = ت³ = – ت

(1+ ت)² = 2 ت   ،    (1 − ت)² = 2− ت 

( ڪ^* ، × ) زمرة إبدالية  محايدها هو (1 ، 0)  ونظير ع هو ع^–1 حيث أن:

                                               س                   − ص

ع = ( س ، ص ) فإن ع^–1 = ( ــــــــــــــــــــــــ ،  ــــــــــــــــــــــــ ) ' ڪ^*  بالطبع ع ع^–1 = و المحايد حيث و = (1 ، 0)

                                          س² + ص²       س² + ص²

إن عملية الضرب تتوزع على عملية الجمع بمعنى:

ع₁(ع₂ + ع₃) = ع₁ع_{2 +} ع₁ع₃  وعليه يكون ( ڪ^* ، + ، × ) حقل الأعداد المركبة

مثال: إذا كان ع₁ = ( 2 ، 3 ) ، ع₂ = ( 3 ، –4 ) فأوجد 25ع₁(ع₂)^–1– ع₁ .

الحل: نوجد النظير ألضربي للعدد ع₂

                                                   3            – (–4)           3        4           1

ع₂ = ( 3 ،  –4 ) فإن (ع₂)^–1 = ( ـــــــــــــــــ ،  ـــــــــــــــــ ) = ( ــــــــ ،  ـــــــ ) = ــــــــ (3، 4) ، 25(ع₂)^–1 = (3 ،4)

                                               9 + 16      9 + 16           25     25        25

ع₁×25(ع₂)^–1 = ( 2 ، 3 ) ( 3 ، 4) = ( 2 × 3 – 3 × 4 ،  2 × 4  + 3 × 3 ) = (–6 ، 17)

 25ع₁(ع₂)^–1 – ع₁ = (–6 ، 17) – ( 2 ، 3 ) = ( –8 ، 14)

حل آخر: ع₁ = 2 + 3ت ، ع₂ = 3 –4ت

                                                           1

25ع₁(ع₂)^–1 – ع₁  = 25(2 + 3ت) × ــــــــــــــــ  – ( 2 + 3ت )

                                                       3 –4ت

                                                            (3 + 4ت)

25ع₁(ع₂)^–1 – ع₁  = 25(2 + 3ت) × ـــــــــــــــــــــــــــــــــــــ  – ( 2 + 3ت )            الضرب × المرافق

                                                       (3 –4ت)(3 + 4ت)

                                                        3+ 4ت

25ع₁(ع₂)^–1 – ع₁  = 25(2 + 3ت) ×  ــــــــــــــــ  –2 –3ت

                                                        9 + 16

                             = (2 + 3ت)(3 + 4ت) –2 –3ت

                             = 6 –12 + 17ت –2 – 3ت

                             = – 8 + 14ت

                             = ( –8 ، 14)